Ponyo's Heat tube: Unterschied zwischen den Versionen
OlegS (Diskussion | Beiträge) |
DHE (Diskussion | Beiträge) |
||
| (84 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
==Thema == | ==Thema == | ||
Ein von oben verschlossenes Glasrohr wird mit Wasser gefüllt und senkrecht aufgestellt. Anschließend wird das untere Ende in ein mit Wasser gefülltes Becherglas getaucht. Wird nun ein kurzes Segment des Rohrs erhitzt, so bilden sich in periodischen Abständen Gasblasen, die nach sehr kurzer Zeit wieder kollabieren. Diese Blasen füllen nahezu den gesamten Querschnitt des Rohres aus und sind mehrere Zentimeter lang. Dies führt zu einem periodischen Austreten von Wasser aus dem offenen Ende, welches anschließend beim Kollabieren der Blase wieder in das Rohr zurückgezogen wird. Diesen Effekt haben wir unter folgender Aufgabenstellung bearbeitet: | |||
''"A glass tube with a sealed top is filled with water and mounted vertically. The bottom end of the tube is immersed in a beaker of water and a short segment of the tube is heated. Investigate and explain the periodic motion of the water and any vapour bubbles observed."'' | |||
==Phänomen== | |||
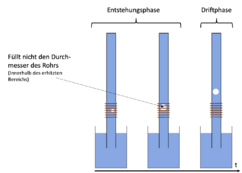
[[Datei:Entstehungsphase+Driftphase PHT.png|mini|242x242px|Entstehungsphase und Driftphase (ohne Taylor-Bubble Entstehung)]] | |||
Wird das Glasrohr an der mit einer Wärmequelle versehenen Stelle hinreichend erhitzt, so bilden sich Dampfblasen, welche, solange sie sich im erhitzten Bereich befinden, wachsen, weil weiterhin Wasser in die Blase verdampft wird (Entstehungsphase). Steig die Blase weiter auf und verlässt die erhitzte Stelle, so driftet sie weiter und kollabiert anschließend (Driftphase). | |||
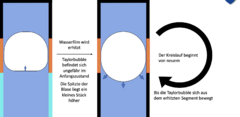
Wächst die Dampfblase hingegen während der Entstehungsphase weit genug an, den um den gesamten Durchmesser auszufüllen, während sie sich noch in der erhitzten Zone befindet, dann bildet sich eine Taylorbubble (eine Gasblase, die nahezu den gesamten Querschnitt eines Rohrs ausfüllt). Diese steigt nur langsam auf, da nur wenig Wasser an ihr vorbeifließen kann. | |||
<gallery widths="240px" perrow="3" heights="160px"> | |||
Datei:TaylorBubble PeriodenEnde PHT.png|rechts|rahmenlos| | |||
Datei:TaylorBubble 2 PHT.png|zentriert|rahmenlos| | |||
Datei:TaylorBubble Entstehung PHT.png|links|rahmenlos| | |||
</gallery> | |||
Gleichzeitig wird der dünne Wasserfilm (nach Literaturwerten < 0,5mm), der sich zwischen der Blase und dem Rohr bildet, immer wieder verdampft, wonach Wasser wieder nachfließt, was zu einer Druckoszillation in der Blase führt. Dies erzeugt die Volumenoszillation. Verlässt die Blase schließlich den erhitzen Bereich, so wird keine weitere Energie mehr hinzugegeben und daher geht die Blase dann in die Driftphase über. | |||
[[Datei:Alle3Phasen PHT.png|zentriert|663x663px|mini|Alle drei Phasen zusammen]] | |||
==Theorie== | ==Theorie== | ||
Aufgrund der Natur des Projektes war es uns nicht möglich einen quantitativen Ansatz zu verfolgen, dennoch lässt sich mit qualitativen Betrachtungen ein tiefer Einblick in das Projekt gewinnen. | |||
== | |||
====Druckbetrachtung==== | |||
Qualitativ kann Wasser als ein ideales Gas verstanden werden und dessen Zustand lässt sich deshalb mit der idealen Gasgleichung darstellen: | |||
$$p \cdot V=n \cdot R \cdot T\\ p_\infty = n \cdot \frac{T}{V}$$ | |||
Es folgt, dass der Druck in der Blase proportional zur Stoffmenge, und Temperatur und antiproportional zu Druck ist. Die Kraftwirkung der Blase auf die Wassersäule ist daher ungefähr: | |||
<nowiki>$$F_b = (n \cdot R \cdot \frac{T}{V} - p_\infty) \cdot A$$</nowiki> | |||
Gleichzeitig wirkt die Wassersäule unter der Taylorbubble eine abwärtsgerichtete Kraft auf die Blase durch den Schweredruck: | |||
<nowiki>$$p = \rho_w \cdot g \cdot h \Leftrightarrow F_s = \rho_w \cdot g \cdot V$$</nowiki> | |||
Nur wenn die Kräfte gleich groß sind, verweilt der untere Rand der Blase in Ruhe. | |||
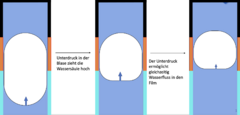
Dies erklärt die näherungsweise periodische Bewegung der Dampfblase. Bildet sich eine kleine Taylorbubble, so entsteht der besagte dünne Wasserfilm, welcher sehr schnell erhitzt, also verdampft wird, da er nicht vom Umgebungswasser gekühlt wird. Dies führt durch die Erhöhung der Stoffmenge nach der idealen Gasgleichung zu einer Druckerhöhung. | |||
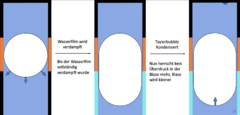
Da das obere Ende des Rohrs verschlossen ist, kann Wasser nur nach unten hin verdrängt werden. Dies geschieht so lange, bis der Wasserfilm vollständig verdampft wurde. Die Temperatur des Wassers in der Blase steigt nicht weiter, deshalb erhöht sich der Druck dadurch auch nicht. Da sich die Gasblase zu diesem Moment allerdings noch ausdehnt und Wasser an der kalten Stelle des Rohrs kondensiert, sinkt der Druck in der Blase. Deshalb kann Wasser an ihr vorbei in den Wasserfilm strömen. Dieses wird anschließend wieder sehr schnell verdampft, weshalb der Druck wieder steigt, weshalb sich der Prozess wiederholt. | |||
====Wärme/Energiebetrachtung==== | |||
Untersucht man den Prozess unter dem Gesichtspunkt des Wärmeflusses, so lassen sich weitere Rückschlüsse auf den Effekt ziehen. Die Formel für den Wärmefluss ist: | |||
<big>$$\frac{dQ}{dt}=\frac{k \cdot A \cdot \Delta T}{l}$$</big> | |||
Wobei die Wärmeleitkoeffizienten folgenden sind: | |||
<nowiki>$$k_{glas} = 0,84 \frac{J}{s \cdot m \cdot K}$$</nowiki> | |||
<nowiki>$$k_{wasser,f} = 0,67 \frac{J}{s \cdot m \cdot K}$$</nowiki> | |||
<nowiki>$$k_{wasser,g} = 0,025 \frac{J}{s \cdot m \cdot K}$$</nowiki> | |||
Wasser und Glas haben einen Wärmeübertragungskoeffizienten in derselben Größenordnung, wobei Dampf einen sehr viel kleineren hat. Deshalb wirkt in diesem Prozess wie ein Isolator, weshalb die Wärmeleitung zwischen Wasser bzw. Glas und Wasserdampf vernachlässigt werden kann. Deshalb kann der Druck in der Taylorbubble nur durch das Verdampfen von Wasser steigen. Dies erklärt, warum der Druck in der Blase nach dem Aufbrauchen des Wasserfilms abfällt. | |||
==Aufbau== | |||
[[Datei:Aufbau (Ponyo´s Heat tube).jpg|alternativtext=Aufbau (Ponyo´s Heat tube)|mini|235x235px|Aufbau]] | |||
Den Großteil der Experimente haben wir mit einem Glasrohr mit einem Durchmesser von 6 mm und 50 cm Höhe durchgeführt. Dieses haben wir oben mit einem Gasdrucksensor verschlossen. Das Glasrohr wurde mithilfe eines Stativs gehalten. Für das Erhitzen des kurzen Segmentes des Rohrs haben wir einen Nichrom-Draht (awg 29 Ø = 0,28mm) verwendet, welcher in mehreren Windungen angebracht wurde. Der Draht ist mit einer Spannungsquelle verbunden, was eine kontrollierte Einstellung der Leistung des Drahtes ermöglicht. Die Messungen haben wir mit dem oben angebrachten Gasdrucksensor quantifiziert, mit einer Messfrequenz von 100Hz. | |||
== Daten== | == Daten== | ||
====Glasrohr Durchmesseränderung==== | |||
Der Durchmesser des Glasrohrs ist von hoher Bedeutung, da sich nur bei bestimmten Rohrdurchmessern mit unserer Hitzequelle Taylorbubbles bilden können. Ist der Durchmesser des Rohrs zu groß, entsteht ein Strom, in welchem die Gasblasen am Wasser vorbeiströmen können. Ist das Rohr zu dünn, so kann kaum Wasser an der Blase vorbeiströmen, weshalb die Blase ständig erhitzt wird und sich ein Gleichgewichtszustand einstellt, bei welchem die Blase nicht mehr kollabiert. | |||
{| class="wikitable" | |||
!Durchmesser Ø | |||
!Wiederholbar | |||
!Taylor Bubble | |||
|- | |||
!3mm | |||
|nein | |||
|nicht kollabiert | |||
|- | |||
!6mm | |||
|ja | |||
|formed und kollabiert | |||
|- | |||
!10mm | |||
|nein | |||
|nicht formed | |||
|} | |||
====Hitzequelle Positionsänderung==== | |||
[[Datei:Durchsnittliche Höhe über Periodendauer PHT.png|mini|237x237px|Durchschnittliche Höhe in Meter über Periodendauer in Sekunden ]] | |||
Obwohl die Experimente mit verschiedenen Positionen der Hitzequelle keine Proportionalität zur Periodendauer oder zur Taylorbubble Höhe gezeigt haben, ist aus diesen Experimenten deutlich geworden, dass die Höhe der Taylorbubble ungefähr linear proportional zur Periodendauer ist. | |||
====Änderung vom Abstand zwischen Windungen (Energieinput)==== | |||
Experimente mit unterschiedlichen Abständen zwischen den einzelnen Windungen haben gezeigt, dass bei kleineren Abständen auch die durchschnittliche Periodendauer kleiner wird. Die Diagramme zeigen die Position, welche wir durch Videotracking erhalten haben, des oberen und unteren Endes der Taylorbubble zu einem gegebenen Zeitpunkt. Es wird ersichtlich, dass in dem Zeitintervall von 50 Sekunden sich mehr Taylorbubbles bei größerer Windungsdichte bilden. | |||
==Fazit== | ==Fazit== | ||
==== Prozessbeschreibung ==== | ==== Prozessbeschreibung ==== | ||
Durch Erhitzen des Wassers bilden sich anfangs kleine Gasbläschen | Durch Erhitzen des Wassers bilden sich anfangs kleine Gasbläschen, bis eine Gasblase so groß wird, dass sie nahezu den gesamten Querschnitt des Rohres ausfüllt (solch eine Gasblase wird auch als Taylor Bubble bezeichnet). Es bildet sich ein dünner Wasserfilm zwischen der Blase und der Innenwand des Rohrs. Dieser Wasserfilm wird von der Rohrinnenwand erhitzt und verdampft. Der Druck in der Blase steigt, bis der gesamte Wasserfilm verdampft ist. Die Blase dehnt sich daher aus und verdrängt Wasser von der erhitzten Stelle aus dem offenen Ende des Rohrs, bis der Umgebungsdruck dem Druck in der Gasblase entspricht. Dem System wird nun weniger Energie hinzugegeben, da der Wärmeübertragungskoeffizient von Gasen kleiner ist, als der von Flüssigkeiten. Weiterhin kondensiert Wasserdampf an den nicht erhitzten Stellen des Glases und an den Phasengrenzen zum abkühlenden Wasser. Dies führt zu einer Drucksenkung in der Gasblase, weshalb die Blase kollabiert. Hierbei wird nun kaltes Wasser aus dem Becherglas durch das offene Ende hineingezogen, was zu einer weiteren Abkühlung des Systems führt. Dann wird das Wasser wieder durch die Wärmequelle erhitzt und der Vorgang beginnt von neuem. | ||
==== Energiebilanz ==== | ==== Energiebilanz ==== | ||
| Zeile 38: | Zeile 102: | ||
Der Energieverlust durch Wärmeleitung kann mit der Formel für Wärmeübertragung quantifiziert werden, hierbei sind T<sub>1</sub>, T<sub>2</sub> die Temperaturen der beiden Körper und der Umwelt zwischen welchen Wärme übertragen wird. | Der Energieverlust durch Wärmeleitung kann mit der Formel für Wärmeübertragung quantifiziert werden, hierbei sind T<sub>1</sub>, T<sub>2</sub> die Temperaturen der beiden Körper und der Umwelt zwischen welchen Wärme übertragen wird. | ||
<nowiki>$$Q_L = \alpha · A · (T_1 − T_2)$$</nowiki> | |||
==Erfolge== | ==Erfolge== | ||
| Zeile 47: | Zeile 111: | ||
*1. Platz Teamwertung BeGYPT ([[Robin Schulze-Tammena]], [[Fabian Schmidt]]) | *1. Platz Teamwertung BeGYPT ([[Robin Schulze-Tammena]], [[Fabian Schmidt]]) | ||
==Quellen== | ==Quellen== | ||
[1] Lehrbuch Physik der Naturwissenschaften und Technik 8.Auflage ISBN: 978-3–662-58280-0 | |||
[2] <nowiki>https://www.isabellenhuette.de/fileadmin/Daten/Praezisionslegierungen/Datenblaetter_Widerstand/ISAOHM.pdf</nowiki> | |||
[3] Robert Thomas Dobson, Theoretical and experimental modelling of an open oscillatory heat pipe including gravity | |||
[4] Natural convection heat transfer inside an open vertical pipe: Influences of length, diameter and Prandtl number | |||
==Danksagung== | ==Danksagung== | ||
Wir bedanken uns bei: | Wir bedanken uns bei: | ||
*Herrn Ebert für | *Herrn Ebert für die tatkräftige Unterstützung bei der Erschließung des Phänomens und für die Hilfe beim Erwerb der Sensoren | ||
*Anja Dücker für | *Anja Dücker für einen immerwährenden Ideenreichtum und handwerklicher Expertise bei der Erstellung vom Versuchsaufbauten | ||
*Antonia Macha für die Idee den Effekt mit Drucksensoren zu untersuchen. | |||
Aktuelle Version vom 23. Juni 2023, 14:29 Uhr
Dieser Artikel handelt vom Projekt "Ponyo's Heat tube" von Oleg Solovyev (18), Nikolaj Sankov (16) und Robin Schulze-Tammena (17). Im Schuljahr 2022/23 haben wir das 13. Projekt des German Young Physicists' Tournament (GYPT) "Ponyo's Heat tube" im Rahmen des PhyZ Kurses am Herder-Gymnasium bearbeitet.
Thema
Ein von oben verschlossenes Glasrohr wird mit Wasser gefüllt und senkrecht aufgestellt. Anschließend wird das untere Ende in ein mit Wasser gefülltes Becherglas getaucht. Wird nun ein kurzes Segment des Rohrs erhitzt, so bilden sich in periodischen Abständen Gasblasen, die nach sehr kurzer Zeit wieder kollabieren. Diese Blasen füllen nahezu den gesamten Querschnitt des Rohres aus und sind mehrere Zentimeter lang. Dies führt zu einem periodischen Austreten von Wasser aus dem offenen Ende, welches anschließend beim Kollabieren der Blase wieder in das Rohr zurückgezogen wird. Diesen Effekt haben wir unter folgender Aufgabenstellung bearbeitet:
"A glass tube with a sealed top is filled with water and mounted vertically. The bottom end of the tube is immersed in a beaker of water and a short segment of the tube is heated. Investigate and explain the periodic motion of the water and any vapour bubbles observed."
Phänomen
Wird das Glasrohr an der mit einer Wärmequelle versehenen Stelle hinreichend erhitzt, so bilden sich Dampfblasen, welche, solange sie sich im erhitzten Bereich befinden, wachsen, weil weiterhin Wasser in die Blase verdampft wird (Entstehungsphase). Steig die Blase weiter auf und verlässt die erhitzte Stelle, so driftet sie weiter und kollabiert anschließend (Driftphase).
Wächst die Dampfblase hingegen während der Entstehungsphase weit genug an, den um den gesamten Durchmesser auszufüllen, während sie sich noch in der erhitzten Zone befindet, dann bildet sich eine Taylorbubble (eine Gasblase, die nahezu den gesamten Querschnitt eines Rohrs ausfüllt). Diese steigt nur langsam auf, da nur wenig Wasser an ihr vorbeifließen kann.
Gleichzeitig wird der dünne Wasserfilm (nach Literaturwerten < 0,5mm), der sich zwischen der Blase und dem Rohr bildet, immer wieder verdampft, wonach Wasser wieder nachfließt, was zu einer Druckoszillation in der Blase führt. Dies erzeugt die Volumenoszillation. Verlässt die Blase schließlich den erhitzen Bereich, so wird keine weitere Energie mehr hinzugegeben und daher geht die Blase dann in die Driftphase über.
Theorie
Aufgrund der Natur des Projektes war es uns nicht möglich einen quantitativen Ansatz zu verfolgen, dennoch lässt sich mit qualitativen Betrachtungen ein tiefer Einblick in das Projekt gewinnen.
Druckbetrachtung
Qualitativ kann Wasser als ein ideales Gas verstanden werden und dessen Zustand lässt sich deshalb mit der idealen Gasgleichung darstellen:
$$p \cdot V=n \cdot R \cdot T\\ p_\infty = n \cdot \frac{T}{V}$$
Es folgt, dass der Druck in der Blase proportional zur Stoffmenge, und Temperatur und antiproportional zu Druck ist. Die Kraftwirkung der Blase auf die Wassersäule ist daher ungefähr:
$$F_b = (n \cdot R \cdot \frac{T}{V} - p_\infty) \cdot A$$
Gleichzeitig wirkt die Wassersäule unter der Taylorbubble eine abwärtsgerichtete Kraft auf die Blase durch den Schweredruck:
$$p = \rho_w \cdot g \cdot h \Leftrightarrow F_s = \rho_w \cdot g \cdot V$$
Nur wenn die Kräfte gleich groß sind, verweilt der untere Rand der Blase in Ruhe. Dies erklärt die näherungsweise periodische Bewegung der Dampfblase. Bildet sich eine kleine Taylorbubble, so entsteht der besagte dünne Wasserfilm, welcher sehr schnell erhitzt, also verdampft wird, da er nicht vom Umgebungswasser gekühlt wird. Dies führt durch die Erhöhung der Stoffmenge nach der idealen Gasgleichung zu einer Druckerhöhung.
Da das obere Ende des Rohrs verschlossen ist, kann Wasser nur nach unten hin verdrängt werden. Dies geschieht so lange, bis der Wasserfilm vollständig verdampft wurde. Die Temperatur des Wassers in der Blase steigt nicht weiter, deshalb erhöht sich der Druck dadurch auch nicht. Da sich die Gasblase zu diesem Moment allerdings noch ausdehnt und Wasser an der kalten Stelle des Rohrs kondensiert, sinkt der Druck in der Blase. Deshalb kann Wasser an ihr vorbei in den Wasserfilm strömen. Dieses wird anschließend wieder sehr schnell verdampft, weshalb der Druck wieder steigt, weshalb sich der Prozess wiederholt.
Wärme/Energiebetrachtung
Untersucht man den Prozess unter dem Gesichtspunkt des Wärmeflusses, so lassen sich weitere Rückschlüsse auf den Effekt ziehen. Die Formel für den Wärmefluss ist:
$$\frac{dQ}{dt}=\frac{k \cdot A \cdot \Delta T}{l}$$
Wobei die Wärmeleitkoeffizienten folgenden sind:
$$k_{glas} = 0,84 \frac{J}{s \cdot m \cdot K}$$
$$k_{wasser,f} = 0,67 \frac{J}{s \cdot m \cdot K}$$
$$k_{wasser,g} = 0,025 \frac{J}{s \cdot m \cdot K}$$
Wasser und Glas haben einen Wärmeübertragungskoeffizienten in derselben Größenordnung, wobei Dampf einen sehr viel kleineren hat. Deshalb wirkt in diesem Prozess wie ein Isolator, weshalb die Wärmeleitung zwischen Wasser bzw. Glas und Wasserdampf vernachlässigt werden kann. Deshalb kann der Druck in der Taylorbubble nur durch das Verdampfen von Wasser steigen. Dies erklärt, warum der Druck in der Blase nach dem Aufbrauchen des Wasserfilms abfällt.
Aufbau
Den Großteil der Experimente haben wir mit einem Glasrohr mit einem Durchmesser von 6 mm und 50 cm Höhe durchgeführt. Dieses haben wir oben mit einem Gasdrucksensor verschlossen. Das Glasrohr wurde mithilfe eines Stativs gehalten. Für das Erhitzen des kurzen Segmentes des Rohrs haben wir einen Nichrom-Draht (awg 29 Ø = 0,28mm) verwendet, welcher in mehreren Windungen angebracht wurde. Der Draht ist mit einer Spannungsquelle verbunden, was eine kontrollierte Einstellung der Leistung des Drahtes ermöglicht. Die Messungen haben wir mit dem oben angebrachten Gasdrucksensor quantifiziert, mit einer Messfrequenz von 100Hz.
Daten
Glasrohr Durchmesseränderung
Der Durchmesser des Glasrohrs ist von hoher Bedeutung, da sich nur bei bestimmten Rohrdurchmessern mit unserer Hitzequelle Taylorbubbles bilden können. Ist der Durchmesser des Rohrs zu groß, entsteht ein Strom, in welchem die Gasblasen am Wasser vorbeiströmen können. Ist das Rohr zu dünn, so kann kaum Wasser an der Blase vorbeiströmen, weshalb die Blase ständig erhitzt wird und sich ein Gleichgewichtszustand einstellt, bei welchem die Blase nicht mehr kollabiert.
| Durchmesser Ø | Wiederholbar | Taylor Bubble |
|---|---|---|
| 3mm | nein | nicht kollabiert |
| 6mm | ja | formed und kollabiert |
| 10mm | nein | nicht formed |
Hitzequelle Positionsänderung
Obwohl die Experimente mit verschiedenen Positionen der Hitzequelle keine Proportionalität zur Periodendauer oder zur Taylorbubble Höhe gezeigt haben, ist aus diesen Experimenten deutlich geworden, dass die Höhe der Taylorbubble ungefähr linear proportional zur Periodendauer ist.
Änderung vom Abstand zwischen Windungen (Energieinput)
Experimente mit unterschiedlichen Abständen zwischen den einzelnen Windungen haben gezeigt, dass bei kleineren Abständen auch die durchschnittliche Periodendauer kleiner wird. Die Diagramme zeigen die Position, welche wir durch Videotracking erhalten haben, des oberen und unteren Endes der Taylorbubble zu einem gegebenen Zeitpunkt. Es wird ersichtlich, dass in dem Zeitintervall von 50 Sekunden sich mehr Taylorbubbles bei größerer Windungsdichte bilden.
Fazit
Prozessbeschreibung
Durch Erhitzen des Wassers bilden sich anfangs kleine Gasbläschen, bis eine Gasblase so groß wird, dass sie nahezu den gesamten Querschnitt des Rohres ausfüllt (solch eine Gasblase wird auch als Taylor Bubble bezeichnet). Es bildet sich ein dünner Wasserfilm zwischen der Blase und der Innenwand des Rohrs. Dieser Wasserfilm wird von der Rohrinnenwand erhitzt und verdampft. Der Druck in der Blase steigt, bis der gesamte Wasserfilm verdampft ist. Die Blase dehnt sich daher aus und verdrängt Wasser von der erhitzten Stelle aus dem offenen Ende des Rohrs, bis der Umgebungsdruck dem Druck in der Gasblase entspricht. Dem System wird nun weniger Energie hinzugegeben, da der Wärmeübertragungskoeffizient von Gasen kleiner ist, als der von Flüssigkeiten. Weiterhin kondensiert Wasserdampf an den nicht erhitzten Stellen des Glases und an den Phasengrenzen zum abkühlenden Wasser. Dies führt zu einer Drucksenkung in der Gasblase, weshalb die Blase kollabiert. Hierbei wird nun kaltes Wasser aus dem Becherglas durch das offene Ende hineingezogen, was zu einer weiteren Abkühlung des Systems führt. Dann wird das Wasser wieder durch die Wärmequelle erhitzt und der Vorgang beginnt von neuem.
Energiebilanz
Um eine Energiebilanz formulieren zu können, ist von besonderer Wichtigkeit, den Energieinput und den Energieoutput des Systems quantifizieren zu können. Energie geben wir durch den angeschlossenen Heizdraht hinzu, wie beim Aufbau gezeigt. Energie geht in Form von Wärmestrahlung und Wärmeleitung verloren.
Energieverlust
Der Energieverlust durch Wärmeleitung kann mit der Formel für Wärmeübertragung quantifiziert werden, hierbei sind T1, T2 die Temperaturen der beiden Körper und der Umwelt zwischen welchen Wärme übertragen wird.
$$Q_L = \alpha · A · (T_1 − T_2)$$
Erfolge
- 1. Preis Regionalwettbewerb Jugend Forscht
- 3. Preis Landeswettbewerb Jugend Forscht
- 1. Platz BeGYPT (Robin Schulze-Tammena)
- 1. Platz Teamwertung BeGYPT (Robin Schulze-Tammena, Fabian Schmidt)
Quellen
[1] Lehrbuch Physik der Naturwissenschaften und Technik 8.Auflage ISBN: 978-3–662-58280-0
[2] https://www.isabellenhuette.de/fileadmin/Daten/Praezisionslegierungen/Datenblaetter_Widerstand/ISAOHM.pdf
[3] Robert Thomas Dobson, Theoretical and experimental modelling of an open oscillatory heat pipe including gravity
[4] Natural convection heat transfer inside an open vertical pipe: Influences of length, diameter and Prandtl number
Danksagung
Wir bedanken uns bei:
- Herrn Ebert für die tatkräftige Unterstützung bei der Erschließung des Phänomens und für die Hilfe beim Erwerb der Sensoren
- Anja Dücker für einen immerwährenden Ideenreichtum und handwerklicher Expertise bei der Erstellung vom Versuchsaufbauten
- Antonia Macha für die Idee den Effekt mit Drucksensoren zu untersuchen.