Magic Stick Trick: Unterschied zwischen den Versionen
K (→Fazit) |
K |
||
| Zeile 13: | Zeile 13: | ||
==Theorie== | ==Theorie== | ||
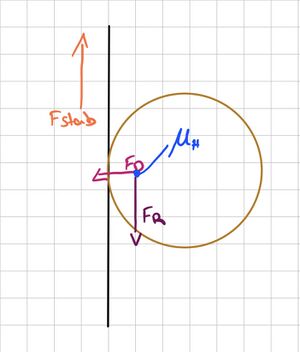
[[Datei:Sandkorn an Stab.jpg|mini|( | [[Datei:Sandkorn an Stab.jpg|mini|(C) Wir sehen ein einzelnes Sandkorn am Stab, mit den dort wirkenden Kräften.]] | ||
Unser Ziel war es ein Minimum $$F_{Stab}$$ mit der Hilfe von $$ \sum_{F_R} $$ zu bestimmen $$(3)$$. $$ F_{Stab} $$ muss größer sein als die gesamt Summe aller Sandkörner $$ \Sigma_{F_R} $$ , damit wir den Stab aus dem Sand ziehen können, müssen wir genügend Kraft aufwenden um die Reibungskraft $$ F_R $$ zu überwinden. | Unser Ziel war es ein Minimum $$F_{Stab}$$ mit der Hilfe von $$ \sum_{F_R} $$ zu bestimmen $$(3)$$. $$ F_{Stab} $$ muss größer sein als die gesamt Summe aller Sandkörner $$ \Sigma_{F_R} $$ , damit wir den Stab aus dem Sand ziehen können, müssen wir genügend Kraft aufwenden um die Reibungskraft $$ F_R $$ zu überwinden. | ||
| Zeile 23: | Zeile 23: | ||
[[Datei:Skizze Flasche mit Sand und Stab.jpg|mini|( | [[Datei:Skizze Flasche mit Sand und Stab.jpg|mini|(D) Es ist zu sehen: eine Flasche mit Sand und Stab und dazu die wirkenden Kräfte.]] | ||
Die Sandkörner sind zwischen Stab und Gefäßwand eingeklemmt. Ein Sandkorn drückt mit $$F_D$$ gegen den Stab. Das passiert von allen Seiten, womit der Stab eingeklemmt wird. Dort wirkt die Haftreibung. Zwischen den Sandkörnern haben wir Kraftbrücken, dass bedeutet, dass die Sandkörner gegen und aufeinander drücken. | Die Sandkörner sind zwischen Stab und Gefäßwand eingeklemmt. Ein Sandkorn drückt mit $$F_D$$ gegen den Stab. Das passiert von allen Seiten, womit der Stab eingeklemmt wird. Dort wirkt die Haftreibung. Zwischen den Sandkörnern haben wir Kraftbrücken, dass bedeutet, dass die Sandkörner gegen und aufeinander drücken. | ||
| Zeile 59: | Zeile 59: | ||
==Aufbau== | ==Aufbau== | ||
[[Datei:Aufbau 2.jpg|mini|( | [[Datei:Aufbau 2.jpg|mini|(E) Durchführung und Aufbau unseres Experimentes]] | ||
Wie schon kurz in unserem Thema erwähnt, brauchen man ein paar Sachen für den Aufbau unseres Projektes. | Wie schon kurz in unserem Thema erwähnt, brauchen man ein paar Sachen für den Aufbau unseres Projektes. | ||
| Zeile 71: | Zeile 71: | ||
==Daten== | ==Daten== | ||
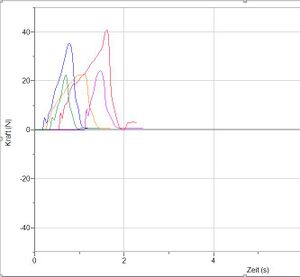
[[Datei:Datengraph .jpg|mini|Graphen zum grauen Sand ]] | [[Datei:Datengraph .jpg|mini|(F) Graphen zum grauen Sand ]] | ||
Hier kommen keine Rohdaten sondern möglichst gut ausgewertete Daten rein - Graphen, Ausgleichskurven, etc. mit Fehlerbetrachtung! | Hier kommen keine Rohdaten sondern möglichst gut ausgewertete Daten rein - Graphen, Ausgleichskurven, etc. mit Fehlerbetrachtung! | ||
Version vom 20. Juni 2023, 17:14 Uhr
Thema
GYPT Aufgabe 12:
Nimm ein Gefäß und schütte etwas körniges Material hinein, zum Beispiel Reis. Wenn man z. B. einen Löffel eintaucht, kann man ab einer bestimmten Eintauchtiefe das Gefäß und den Inhalt anheben, indem man den Löffel festhält. Erklären Sie dieses Phänomen und untersuchen Sie die relevanten Parameter des Systems.
Statt einen Löffel haben wir einen Holzstab benutzt, mit einer Flasche voller Sand. Wir haben das körnige Material variiert mit zwei unterschiedlichen Sandarten und zwei unterschiedlichen Holzstäben.
Basic Explanation
Auf dem Bild ist eine Box auf einer Ebene zusehen. Wenn von der linken Seite eine Kraft gegen die Box drückt, die Box sich aber nicht bewegt, dann haben wir es mit einer Haftreibung zu tun. Das liegt daran das zwischen der Ebene und der Box es uneben ist und somit eine größere Kraft benötigt wird. Ab dem Punkt wo sich die Box bewegt, ist auch keine Haftreibung mehr vorhanden.
Aber wir haben nicht nur die Haftreibung sondern auch den Druck. Auf dem Bild ist ein Wasserbecken zu sehen, mit einer roten Steigung gekennzeichnet. Je tiefer im Wasser desto höher der Druck. Genauso auch auf unserem Experiment zurück zu verfolgen mit Sand.
Theorie
Unser Ziel war es ein Minimum $$F_{Stab}$$ mit der Hilfe von $$ \sum_{F_R} $$ zu bestimmen $$(3)$$. $$ F_{Stab} $$ muss größer sein als die gesamt Summe aller Sandkörner $$ \Sigma_{F_R} $$ , damit wir den Stab aus dem Sand ziehen können, müssen wir genügend Kraft aufwenden um die Reibungskraft $$ F_R $$ zu überwinden.
$$F_R$$ können wir berechnen indem wir $$\mu_h$$, also den Haftreibungskoeffizenten mit $$F_D$$, der Kraft des Drucks multiplizieren $$(2)$$. Das muss für jedes einzelne Sandkorn wiederholt werden.
Weil jedes Sandkorn sein eigenes $$F_D$$, $$F_R$$ und $$\mu_h$$ hat. $$\mu_h$$ ist direkt abhängig von $$F_D$$. Um die unendlich vielen Sandkörner zu berechnen, könnte man Integrale verwenden.
Die Sandkörner sind zwischen Stab und Gefäßwand eingeklemmt. Ein Sandkorn drückt mit $$F_D$$ gegen den Stab. Das passiert von allen Seiten, womit der Stab eingeklemmt wird. Dort wirkt die Haftreibung. Zwischen den Sandkörnern haben wir Kraftbrücken, dass bedeutet, dass die Sandkörner gegen und aufeinander drücken.
Auf jede Aktion folgt eine Reaktion. In unserem Fall ist die Aktion $$F_D$$ und die Reaktion ist die Gegenkraft, die auf die Gefäßwand vom Sand aus wirkt.
$$F_R$$ wirkt nach unten in Richtung Gefäßboden, während unsere Aktion, also $$F_{Stab}$$ nach oben wirkt, da wir den Stab aus der Flasche raus ziehen wollen. $$F_D$$ bestimmen wir indem wir Kraft $$F$$ durch Fläche $$A$$ rechnen $$(1)$$.
Formeln
\begin{align} F_D &= \dfrac{F}{A} \\ F_R &= \mu_h \cdot F_D \\ F_{Stab} &= \sum_{F_R} \\ \end{align}
Formelzeichen:
$$F_D$$:Kraft vom Druck
$$F$$: Kraft
$$A$$: Fläche
$$F_R$$: Reibungskraft
$$\mu_h$$: Haftreibungskoeffizent
$$F_{Stab}$$: Kraft des Stabes
$$\sum$$: Summe
Aufbau
Wie schon kurz in unserem Thema erwähnt, brauchen man ein paar Sachen für den Aufbau unseres Projektes.
Wir haben statt des Löffels, wie eigentlich in der Theorie erwähnt, einen Holzstab benutzt. Zusätzlich benötigt man noch eine Plastikflasche und wir haben unser Material variiert, indem wir zwei unterschiedliche Arten von Sand benutzt haben und zwei Arten von Holzstäben.
Nun zu unserem Aufbau. Zuerst haben wir den Stab bis zu einer bestimmten Eintauchtiefe in die mit Sand gefüllte Flasche gesteckt.
Später haben wir die Eintauchtiefe variiert, indem wir Markierungen (jeweils mit Abstand von 0,2 cm) auf dem Stab gemacht haben. Wenn der Stab also im Sand steckt, haben wir den Sand erstmal verdichtet, sodass der Stab auch im Sand stecken bleibt. Danach haben wir an dem Stab gezogen und so die Flasche angehoben. So setzt sich eigentlich unser ganzes Projekt zusammen.
Um sich das Ganze auch physikalisch erklären zu lassen, schaut bitte in unsere Theorie rein!
Daten
Hier kommen keine Rohdaten sondern möglichst gut ausgewertete Daten rein - Graphen, Ausgleichskurven, etc. mit Fehlerbetrachtung!
Fazit
Durch die ein jährige Bearbeitung und Erforschung unserer physikalischen Problemstellung, haben wir das Experiment erfolgreich nach machen können und konnten damit auf unterschiedliche zu untersuchende Parameter schließen. Wir haben uns schließlich auf nur zwei Parameter beschränkt und diese ausgiebig untersucht und gemessen. Somit könnten wir uns dann einen mathematischen Weg erschließen und daraus eine Theorie mit Formeln bilden.
Zu Beginn haben wir uns zu lang damit aufgehalten zu viele Parameter zu variieren und zu untersuchen. Bei unseren Messungen hätten wir zudem von Anfang an darauf achten sollen, dass wir korrekt und immer unter den gleichen Bedingungen messen, was uns am Ende einiges an Zeit gekostet hat. Wir hätten gerne zum Ende noch korrekte Messungen von mehr als einer Art von Sand gehabt.
Erfolge
Wir haben im Regionalwettbewerb von Jugend forscht einen Sonderpreis gewonnen.
Danksagung
Wir danken Timo Huber für seine tatkräftige Unterstützung bei unserer Theorie. Außerdem danken wir Ulrike Jeschke, Anja Düker und Dr. Falk Ebert für ihre zahlreichen Anregungen.