Magneto-Mechanischer Oszillator
Thema
"Secure the lower ends of two identical leaf springs to a non-magnetic base and attach magnets to the upper ends such that they repel and are free to move. Investigate how the movement of the springs depends on relevant parameters."
Befestigen Sie die unteren Enden zweier identischer Blattfedern an einer nicht magnetischen Basis und befestigen Sie Magnete an den oberen Enden, sodass sie sich abstoßen und sich frei bewegen können. Untersuchen Sie, wie die Bewegung der Federn von relevanten Parametern abhängt.
Theorie
Parameter
Die folgenden Parameter sind benötigt, um den Effekt treffend zu beschreiben:
- die Maße der Feder (Länge, Dicke , Breite, Masse)
- Abstand zwischen den zwei Magneten
- Maße der Magneten (Dipolmoment, Masse)
Die Kräfte die in diesem System wirken, sind:
- Rückstellkraft $$F_R$$
- Magnetkraft $$F_M$$
- Dämpfungskraft $$F_D$$
Grundlegende Erklärung
Wenn man die Federn auslenkt, so wird potentielle Energie gespeichert. Lässt man sie los, so wird diese um gewandelt, in kinetische Energie, sowie in Wärme (wobei dieser Teil minimal ist), durch die Magneten, die an beiden Federn befestigt sind, kann zudem kinetische Energie zwischen den Federn übertragen werde, sodass sich die beiden Schwingungen überlagern. Je nachdem wie die Federn auslenkt kann man verschiedene Schwingungsmuster erkennen, darunter Schwebungen, gedämpfte Kosinusschwingungen sowie komplexere Muster. Je länger die Feder schwingt, desto geringer ist die Frequenz sowie die Amplitude, mit der sie schwingt, da immer mehr Energie an die Luft, durch Luftreibung abgegeben wurde.
Die Feder
Die Feder hat viele Eigenschaften, die für diesen Effekt zu untersuchen sind, hauptsächlich sind jedoch die Biegung der Feder sowie die Rückstellkraft.
Die Biegung der Feder
Die Biegung der Feder lässt sich genau mithilfe der Balkentheorie beschreiben, jedoch reicht es für uns eine Näherung für diese aufzustellen, um diesen Sachverhalt nicht unnötig komplexer zu machen. Um eine Funktion für die Biegung der Feder $$W(x)$$ zu finden, müssen wir einige Bedingungen aufstellen, welche die gesuchte Funktion erfüllen muss.
- $$ W(0) = 0 $$ Da Biegung an der Länge null muss gleich 0 sein, da die Feder dort befestigt sein soll.
- $$ W(L) = 1 $$ An der Stelle L soll die Biegung maximal sein, hier 1, damit man diese gut mit einem weiteren Koeffizienten multiplizieren kann
- $$ \frac {d^2 W(L)} {dx}^2 = 0 $$ Die zweite Ableitung an der Stellen L soll nun sein, da die zweite Ableitung der Biegelinie das Biegemoment ist, welches am Rand der Feder null ist, da dieser umgebogen ist.
Die Funktion die wir nach diesen Kriterien gewählt haben ist $$ W(x) = 1 - \cos(\frac{\pi}{2L}x) $$. Vorab gesagt ist diese Funktion nach den Bedingungen willkürlich gewählt, nach diesen Bedingungen, jedoch passt sie sehr gut, wie man in dem nebenstehenden Diagramm sieht.
Die Rückstellkraft
Die Rückstellkraft lässt sich mithilfe des Hooke'schen Gesetztes beschreiben, jedoch ist zu sagen, dass das Hooke'sche Gesetz den y -Teil der Kraft vernachlässigt, da wir jedoch keine allzugroßen Auslenkungen betrachen, ist dies nicht von großem Belangen
$$ F_R = -k \cdot w \quad w\; - $$ Auslenkung
k ist hier die Federkonstante, sie beschreibt die Steife der Feder. Für diese gilt die folgende Formel, welch man sich ausser Balkentheorie herleiten kann:
$$k = \frac{EI}{L^3} \quad E \; $$- Elastizitätsmodul
Das I beschreibt das Axiale Flächenträgheitsmoment, dies ist eine Querschnittsgröße der Feder, und ist von der Dicke sowie der Breite dieser abhängig.
Die Magnetkraft
Für die Kraft, die zwischen zwei Dauermagneten wirkt gilt die folgende Formel:
$$\begin{equation} \vec{F}(\vec{r},\vec{m}_1,\vec{m}_2)=\frac{3\mu_0}{4\pi r^4} \left[ \vec{m}_2(\vec{m}_1\cdot\vec{r}_n)+ \vec{m}_1(\vec{m}_2\cdot\vec{r}_n)+ \vec{r}_n(\vec{m}_1\cdot\vec{m}_2)- 5\vec{r}_n(\vec{m}_1\cdot\vec{r}_n)(\vec{m}_2\cdot\vec{r}_n) \right] \end{equation} \quad m - $$ magnetisches Moment $$\begin{equation} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad r_n \; - \end{equation} $$ Einheitsvektor der von Magnet 1 zu Magnet 2 zeigt
Diese Formel kann vereinfachen, da wir die Bewegung eindimensional betrachten, sodass man die Vektoren auf als den Betrag mit Vorzeichen Betrachen kann, wodurch man dies erhält:
$$ F= \frac{3\mu_0 m_1 m_2}{2\pi r^4} $$
Mit einer Formel, wie dieser, kann man jedoch keine allgemeinlösbaren Differentialgleichungen aufstellen, sodass wir diese linear annehmen, diese Annahme ist jedoch nur für kleine Ausrenkungen gültig, da sonst eine. zu starke Abweichung entstehen könnte. Daher gilt:
$$ F_M = c(d_0 + w1 + w2) $$
c ist hier der Differenzenquotient zwischen der Magnetkraft die bei dem maximalen abstand und der bei minimalen Abstand zwischen den Magneten wirkt. Und $$d_0$$ ist der Abstand zwischen diesen in Ruhe.
Vereinfachtes Modell
Mithilfe dieser Kräfte kann man ein vereinfachtes Modell erstellen, um diesen Effekt zu beschreiben. Hier vernachlässigen wir die Dämpfung und nehmen zudem kleine Auslenkungen an, um lösbare DGLs zu erhalten. Wir werden hier drei Modell einführen, die drei sind von unterschiedlicher Komplexität, wobei das letzte den betrachteten Effekt darstellt. Die anderen zwei sind jedoch für das weitere Verständnis des Ansatzes, welchen wir verwendet haben sinnvoll.
Freie Biegeschwingung
In diesem Fall Betrachen wir die Schwingung einer ungedampften Blattfeder mit Masse am Rand. Um diese zu beschreiben verwenden wir Newton'sche DGLs, welche man erhält, indem man die auf eine Punktmasse wirkenden Kräfte summiert. Das einzige problem ist, dass wir keine Punktmasse haben. Dies kann man jedoch umgehen, indem man eine effektive Masse berechnet, doch mehr dazu später. Da bei der freien Biegeschwingung, die einzige wirkende Kraft die Rückstellkraft ist gilt hier:
$$ F_{ges} = F_R $$
Umgeformt erhalten wir daher:
$$ \ddot{w} + \frac{k}{m}w = 0 $$
Die Lösung dieser DGL würde hierbei so aussehen:
$$w = \hat w \cdot \cos(\omega_F t) \quad \omega_F = \sqrt{\frac{k}{m}} $$
Schwingung mit festgemachtem Magneten
Hier betrachten wir den Fall, dass man neben der Feder mit magnet einen Magneten festmacht, sodass es auch eine magnetische Kraft gibt, die einwirkt. Daher gilt auch
$$ F_{ges} = F_R +F_M $$
Daraus folgt dann:
$$ \ddot{w} + \frac{k-c}{m}w = 0 $$
Und die Lösung dieser DGL wäre:
$$w = \hat w \cdot \cos(\omega_{FL} t) \quad \omega_{FL} = \sqrt{\frac{k-c}{m}} $$
Gekoppelte Schwingung
Um die Bewegungsgleichung für den gekoppelten Schwinger zu bestimmen, kann man denselben Ansatz wie im 2. Modell nehmen. Denn wirken auch hier nur die Magnetkraft und die Rückstellkraft, da wir jedoch zwei Federn haben, brauchen wir auch zwei Gleichungen um die Bewegung beider zu beschreiben:
$$F_{ges1}=F_{R1} + F_M \\ F_{ges2}= F_{R2} - F_M $$
Diese würden dann so aussehen:
$$ \ddot{w_1} + \frac{k}{m}w_1 - \frac{c}{m}(w_1+w_2+d_0) \\ \ddot{w_2} + \frac{k}{m}w_2 + \frac{c}{m}(w_1+w_2+d_0)$$
Diese zwei DGLs sind gekoppelt, um diese zu lösen, muss man erstmal die Gleichungen entkoppeln, doch ersparen wir dem Leser dies, da dies nicht dem Verständnis hilft und nur Prahlerei wäre, daher schauen die Lösungen der Gleichungen so aus:
$$w_1=\frac 1 2(A_2\cos(\omega_{+}t)-A_1\cos(\omega_{-}t))+\frac {cd} m\ \\ w_2=\frac 1 2(A_2\cos(\omega_{+}t)+A_1\cos(\omega_{-}t))-\frac {cd} m \\$$
$$ \omega_{-}=\sqrt{\frac{k-2c} m}\\ \omega_{+}=\sqrt{\frac k m} $$
$$A_1=\left( \hat{w}_1-\hat{w}_2\right)\\ A_2=\left( \hat{w}_1+\hat{w}_2\right) $$
Hier schwingen die Federn mit zwei Frequenzen, die eine ist hier von der Magnetkraft beeinflusst, die andere nicht.Dies sind die allgemeinen Lösungen der Gleichung, jedoch gibt es noch drei spezifische interessante Fälle, welche man unter bestimmten Anfangsbedingungen erhält.
Fall a
Wenn man die Feder beide Federn gleichzeitig in die selbe Richtung auslenkt, so schwingen die beiden Federn in Phase, die Magnetkraft hat keinen Einfluss. Daher schwingen sie auch nur mit der Frequenz $$\omega_+$$. Hierbei schaut die Bewegungsgleichung so aus:
$$ w_1 = \hat w \cdot \cos(\omega_+ t) = w_2 $$
Fall b
Wenn man die zwei Federn mit demselben Betrag in eine andere Richtung jedoch auslenkt, so hat die Magnetkraft nun einen Einfluss, denn schwingen die Federn durch diese mit der höheren Frequenz $$\omega_-$$. Außerdem Schwingen sie in Gegenphase, da sie auch entgegengesetzt ausgerenkt wurden.
$$ w_1 =\hat w \cdot \cos(\omega_- t) = -w_2 $$
Fall c
Lenkt man nur eine Feder aus, so wird die Energie zwischen den Federn ständig übertragen, sodass die Amplitude immer größer und kleiner wird, man erhält eine Schwebung.
$$ w_1= \hat w \cdot \cos(\frac{\omega_- + \omega_+}{2} t) \cos(\frac{\omega_- - \omega_+}{2} t) \\ w_1 =\hat w \cdot \sin(\frac{\omega_- + \omega_+}{2} t) \sin(\frac{\omega_- - \omega_+}{2} t) $$
Hier schwingen die Feder mit zwei Frequenzen, wobei die eine die Änderung der Amplitude beeinflusst und die andere die Anzahl an Nulldurchgängen.
Die effektive Masse
In der bisherigen Modellierung haben wir oft die Mass m verwendet, ohne tiefer auf diese einzugehen. Denn setzt sich m nicht nur aus der Masse der Magneten $$ m_M$$ zusammen, sondern auch noch aus einen Teil der Masse der Feder, der effektiven Masse. Wir habe diese mithilfe der kinetischen Energie berechnet, denn kann man diese nicht nur von einem Punkt aus berechnen, sondern nur die gesamte kinetische Energie des Balkens. Dafür muss man dann ein Integral verwenden, sodass man die Bewegungsenergie über den gesamten Balken summiert. Daher schaut die kinetische Energie so aus:
$$ E_{kin} = \frac {1}{2} \cdot m_M \cdot {v(L)}^2 + \frac {1}{2} \cdot \int_{0}^{L} {v(x)}^2dm $$
Wobei der Integrant $$ dm $$ sich zusammensetzt aus:
$$ dm = \frac {m_F}{L} \cdot dx \qquad m_F - $$ Masse der Feder
Daraus folgt:
$$ E_{kin} = \frac {1}{2} \cdot m_M \cdot {v(L)}^2 + \frac {1}{2} \cdot \frac {m_F}{L} \cdot \int_{0}^{L} {v(x)}^2dx $$
Nun gilt $$ v(x) = \dot{w} $$ und $$w(x,t) = (1-\cos(\frac{\pi}{2L}x)) \cdot w_L(t)$$, sodass folgt:
$$ E_{kin} = \frac {1}{2} \cdot m_M \cdot {v(L)}^2 + \frac {1}{2} \cdot \frac {m_F}{L} \cdot {v_L(t)}2 \cdot \int_{0}^{L} {(\frac{\pi}{2L} \cdot \cos(\frac{\pi}{2L}x))^2} dx $$
Umgeformt ergibt sich:
$$E_{kin}= \frac {1}{2} (m_M + (\frac {3}{2}- \frac {4}{\pi}) \cdot m_F) \cdot {v_L(t)}^2$$
Sodass man erkennt, dass gilt:
$$m = m_M + (\frac {3}{2}- \frac {4}{\pi}) \cdot m_F = m_M + 0,227 \cdot m_F$$
Dämpfungskraft
Bisher haben wir in unserer Modellierung angedampfte Schwingungen betrachtet, dies hat den Grund, dass wir so eine grobe Beschreibung des Effekts erreichen wollten, und diese so einfach wie möglich halten wollte. Dabei hat die Dämpfung natürlich auch einen Einfluss, jedoch besteht der Kern des Effekts in der Wechselwirkung der zwei Federn durch die Magneten. Gäbe es keine Dämpfung, so würde dieser Effekt für immer fortwähren, da wir jedoch diese nicht isolieren, ist die Dauer endlich.
Die Dämpfungskraft ist, in unserem Fall, abhängig von der Dämpfung. Je schneller die Feder, desto höher die Dämpfungskraft, desto mehr Energie wird abgegeben. Bei dem Federschwinger entsteht die Dämpfung hauptsächlich durch die Luftreibung. Für die Luftreibung gilt folgende Formel:
$$ F_L = \frac{1}{2} \cdot c_w \cdot \rho_{Luft} \cdot A \cdot {v(t)}^2 \qquad A \; - $$ Angriffsfläche
Jedoch gilt diese Formel nur für Körper, die sich an jeder Stelle mit der gleichen Geschwindigkeit bewegen, im unserem Fall jedoch bewegt sich die Feder nicht einheitlich, an der Stelle $$x = 0$$ ist $$v = 0$$, bei $$x = L$$ gilt $$v = \hat v$$. Daher müssen wir in unserem Fall die Dämpfungskraft über den ganzen Balken summieren, wir nehmen das Integral, dieses würdedann so aussehen:
$$ F_D = \frac{1}{2} \cdot c_w \cdot \rho_{Luft} \cdot A \cdot \int_{0}^{L} {v(x,t)}^2dx $$
Um dieses Integral zu lösen, können wir auch hier den Ansatz $$ v = \dot w $$ und $$ w(x,t) = W(x) \cdot w_L(t) $$ verwenden, sodass wir folgendes erhalten:
$$ F_D = \frac{1}{2} \cdot c_w \cdot \rho_{Luft} \cdot A \cdot {v_L(t)}^2 \cdot \int_{0}^{L} {(\frac{\pi}{2L} \cdot \cos(\frac{\pi}{2L}x))^2} dx $$
Und durch Lösen des Integrals erhält man:
$$ F_D = \frac{1}{2} \cdot c_w \cdot \rho_{Luft} \cdot A \cdot (\frac {3}{2}- \frac {4}{\pi}) \cdot L \cdot {v_L(t)}^2 = \delta \cdot {v_L(t)}^2 $$
Vollständiges Modell
Nun da wir die Dämpfungskraft haben, können wir diese auch in die Gleichungen integrieren, jedoch wären diese Differentialgleichungen sowieso schon unlösbar, sodass wir auch die eigentliche Formel für die Magnetkraft verwenden können.
Daher gilt für die einfache Biegeschwingung:
$$ \ddot w + \frac {k}{m} w - \frac {\delta}{m} {\dot w}^2 = 0 $$
Für die Biegeschwingung mit festem Magneten gilt:
$$ m \ddot w = - k w + \frac {c_M}{(d_0 + w)^4} + \ {\dot w}^2 \qquad \quad c_M \;- $$ Proportionalitätskonstante für die Magnetkraft
Und für die gekoppelten Biegeschwingungen gilt:
$$m_1 \ddot w_1 = -k{w_1} - \frac {c_M}{(d_0 + w_1 + w_2)^4} + \delta {\dot w_1}^2 \\ m_2 \ddot w_2 = -k{w_2} - \frac {c_M}{(d_0 + w_1 + w_2)^4} + \delta {\dot w_2}^2 $$
Diese DGLs sind nicht lösbar, weshalb wir sie numerisch simuliert haben mithilfe von Octave.
Simulation
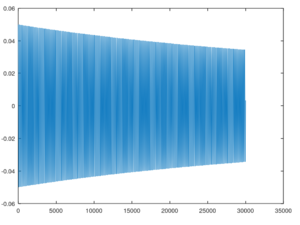
Zur Simulation wollten wir ürsprünglich LSODE oder einen anderen Differentialgleichungslöser verwenden, jedoch konnten wir die Gleichungen aufgrund der Potenten nicht aufstellen, sodass wir stattdessen, nach demselben Prinzip haben wir den Prozess für ein kleines Zeitintervall (1ms) linear angenommen, und haben so für viele verschiedene Zeitpunkte den ungefähren Verlauf vorhergesagt.
Dadurch erhalten wir Plots, wie den neben stehenden, jedoch ist die Dämpfung bei diesen sehr gering für den beschriebenen Fall, mögliche Ursprünge dieser Abweichung, sind, dass wir einen Einheitenfehler in der Simulation haben, oder, dass wir einen großen Teil der Dämpfung vernachlässigen, jedoch haben wir den Ursprung des Fehlers noch nicht gefunden.
Bei den zwei anderen Simulationen kam noch dazu, dass die Koeffizienten für die Magnetkraft zu grob und ungenau waren, sodass die Simulation nicht für alle Federlängen und Abstände funktioniert hat, weshalb wir der Meinung sind, dass diese Werte nicht aussagekräftig sind.
Aufbau
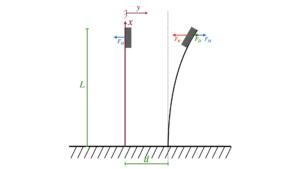
Aufbau zur Untersuchung des Effekts
Dies ist der Aufbau, mit dem wir diesen Effekt untersucht haben. An diesem kann man sowohl die Länge der Feder, als auch die Distanz zwischen den Federn verändern, sodass man sowohl den Einfluss von Magnetkraft, als auch von der Rückstellkraft gesondert betrachten kann. Der einzige Nachteil an diesem Aufbau ist, das dieser Teils aus Metall besteht, was aufgrund von den Magneten unpassend sein könnte, jedoch sind wir der Meinung, dass dieser Einfluss vernachlässigter ist, da die Magnetkraft mit so einer hohen Potenz abnimmt, sodass sie auf die Metallstäbe keinen Einfluss hat.
Um Daten zu sammeln habe wir hall Sonden in der Nähe der Magneten befestigt, um die Änderung des magnetischen Flusses zu beobachten. Denn konnten wir dies anhand der Vernier - Labquest Technologie sehr einfach und zeiteffizient. Dies kam leider auf Kosten davon, dass wir die Auswirkungen auf die Amplitude mit diesen Messungen nicht betrachen können, da die Feldstärke sich nicht linear ändert. Jedoch konnte man dank der hohen Auflösung der Hall Sonden gute Aussagen über die Frequenz treffen, welche wir mithilfe einer Fast - Fourier - Transformation bestimmen konnten. Um weiterhin eine Aussage über die Dämpfung und die Amplitude der Schwingung treffen zu können, haben wir Videomessungen durchgeführt und diese mithilfe des VIdeotrackingprogramms Tracker ausgewertet. Zur Aufnahme der Videos haben wir die Kamera eines iPhone 11 benutzt und haben diese im Slow - Mo Modus aufgenommen, welcher eine Bildrate von 240 fps liefert.
Aufbau zur Messung der Rückstellkraft der Blattfeder
Um die Rückstellkraft der Feder zu messen, haben wir mithilfe eines Vernier - Kraftsensors eine Kraft auf die Feder ausgeübt, wodurch auch eine Gegenkraft auf den Sensor wirkte, dabei haben wir die Feder immer genau um einen bestimmten betrag ausgelenkt
Aufbau zur Messung der Magnetkraft
Um die Magnetkraft zu messen, haben wir auch hier einen Vernier - Kraftsensor benutzt, und einen Magneten an diesen befestigt. Mit dem anderen Magneten sind wir dann dem befestigen näher gekommen, und haben die Distanz zwischen diesen notiert.
Daten
Messung der Federkonstante
Im Diagramm für die Federkraft kann man eine abfallende Expotenzialkurve beobachten. Dies sagt uns, dass mit größerer Effektivlänge der Feder die Federkonstante steigt. Durch einen log-log-Plot, konnte man erkennen, dass es eine Proportionalität von $$k \sim \frac{1}{l^3}$$ existiert.
Als eine Fehlerabschätzung hat der Kraftsensor bei einer Kraft von unter 50N einen Fehler von $$±0.05\,N$$(Quelle [1]). Da wir den Durchschnitt von 5 verschiedenen Auslenkungen für jede effektive Federlänge genommen haben, sollte der Fehler in Abmessung der Auslenkung vernachlässigbar sein.
Messung der Magnetkraft
Im Diagramm für die Messung der Magnetkraft über Abstand sieht man auch eine expotenziell abfallende Kurve. Diese kann man durch die Abhängigkeit $$d \sim \frac{1}{d^4}$$ beschreiben. Dies gibt uns den zusammenhang, dass die Magnetkraft mit vergrößerung der Distanz stark abnimmt.
Der Fehler ist der gleiche wie bei der Messung davor. Der Kraftsensor misst auch mit der Genauigkeit $$\pm0.05N$$(Quelle [1]). Die Distanz zwischen den Magneten können wir auf $$\pm0.5 mm$$ genau bestimmen. Insgesammt ist die Messung aber ungenauer, da der Kraftsesnor höhstwahrscheinlich mit Magneten arbeitet, was unsere Messung beeinflussen könnte.
Messung der Frequenz
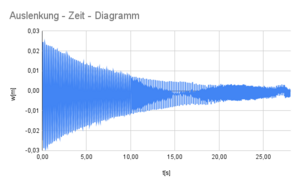
Im allgemeinen kann man sagen, dass eine Schwebung zu beobachten ist. Diese haben wir dann mithilfe von einer Fast-Fourier-Analyse bearbeitet und verschiedene Schwingungsfrequenzen bekommen.
Messung der Auslenkung
Wir haben verschiedene Auslenkungen probiert, doch dies hat die Frequenz der Schwebung nicht verändert. Es hat die Höhe der nachfolgenden Amplituden verändert, doch das konnten wir schlecht mit Hall-Sonden messen. Da es keinen Einfluss auf die Frequenz hatte, haben wir in den folgenden Experimenten eine beliebige Auslenkung benutzt.
Messung mit Veränderung der Federkonstante
Die Messungen für die Veränderung der Federkonstante zeigen, dass eine größere Federkonstante eine größere Frequenz verursacht. Dies stimmt mit unserer Theorie überein, da bei der Berechnung von $$\omega_+$$ und $$\omega_-$$ das k im Nenner steht. Die Messungen stimmen aber immer noch nicht mit den Theoriewerten überein. Die berechneten Werte haben eine Ähnliche Entwicklung wie die gemessenen Werte, sind aber viel höher, da wir in der Theorie bei der berechnung die Dämpfung vernachlässigt haben.
Um unsere Theorie trotzden zu überprüfen haben wir uns die Formeln für die einfachen Fälle mit einzelnen Oszillatoren. Wir haben gesehen, dass man den Formeln nach die Frequenzen der Schwebung, $$\omega_+$$ und $$\omega_-$$, durch die Frequenzen der einzelnen Oszillatoren, $$\omega_f$$ und $$\omega_{fl}$$, berechnen lassen.
\begin{align} \omega_+ &=\sqrt{\frac{k}{m}}\\ \omega_- &=\sqrt{\frac{k-2c}{m}}\\ \omega_f &=\sqrt{\frac{k}{m}}\\ \omega_{fl} &=\sqrt{\frac{k-c}{m}}\\ \Rightarrow\\ \omega_+ &= \omega_f\\ \omega_- &= \omega_{fl}^2-\omega_{f}^2 \end{align}
Der Vergleich dieser vier Frequenzen gibt uns eine sehr gute Übereinkunft und bestätigt unsere Theorie. Es sagt uns auch, dass unsere Frequenz sehr stark von der Dämpfung beeinflusst wird, die wir wenig betrachtet haben.
Als erste Fehlerquelle haben wir Die Abmessung der effektiven Federlänge, die wir nur auf max 1 mm genau einspannen können. Die andere Fehlerquelle ist die FFT-Transformation, die maximal Frequenzen betrachten kann, die hälfte der Messauflösung groß sind. Bei einer Messauflösung von 1000 Messungen pro Sekunde und Frequenzen von ungefähr 10Hz und kleiner.
\begin{align} \frac{1000Hz}{ 2} = 500Hz\\ \frac{10Hz}{500Hz} = \frac{1}{50} = 2\% \end{align}
Der Fehler ist also $$\pm 2 \%$$.
Den Fehler der Hall-Sonde können wir ignorieren, weil dieser nur maximal $$\pm 0.004 mT$$(Quelle [2]) betragen und dies in der Fourier-Analyse nur als rauschen identifiziert wird.
Messung mit Veränderung der Distanz
Im Diagramm für die Distanzveränderung können wir deutlich sehen, dass sich nur eine Frequenz verändert und die andere konstant bleibt. Dies stimmt auch mit unsrer Theorie überein, da nur $$\omega_-$$ von der Magnetkraft abhängt und $$\omega_+$$ nicht. Man sieht auch, dass $$\omega_-$$ zu $$\omega_+$$ konvergiert, was auch logisch ist, da beide gleich wären, wenn die Magnetkraft gleich Null ist.
Die Fehler hierbei sind die gleiche wie beim Experiment zuvor, da wir den Abstand zwischen den Klemmen, die die Federn halten auf $$ \pm 0.5mm $$ genau bestimmen können. Der Fehler der Hall-Sonden wird wie zuvor von der Fourier Analyse als Rauschen aufgenommen und es zählt der Fehler der Fourier-Analyse.
Messung mit Veränderung der Masse
Für die Massemessung haben wir die Masse von einer und dann von 2 Federn gleichzeitig verändert. Auf den Diagrammen sieht man, dass die Frequenz des Schwingers mit der veränderten Masse kleiner wird. Der Fall mit 2 Massen stimmt mit unserer Theorie überein, da die masse im Nenner steht. Darum wird die Frequenz kleiner, wenn die Masse größer wird.
Als Fehler bleiben die $$2\%$$ der fourier analyse bleiben bestehen und der Fehler bei der Abmessung der Masse beträgt c.a. $$\pm 0.01 g$$, da wir die Knete mit einer sehr genauen Waage abgewogen haben, die auf 2 Stellen nach dem Gramm wiegt.
Fazit
Erfolge
- Jugend Forscht Interdisziplinärer Preis in der Regionalrunde und Teilnahme an der Landesrunde (Egor, Nicolas, Uladzimir)
- 13. Platz in der Bundesrunde GYPT(Uladzimir)
- X. Platz in der Bundesrunde GYPT(Nicolas)
- 17. Platz in der Bundesrunde GYPT(Daniel)
Quellen
Eure wichtigsten verwendeten Quellen mit Verweisen im Text!