Magic Stick Trick

Thema

GYPT Aufgabe 12:

Nimm ein Gefäß und schütte etwas körniges Material hinein, zum Beispiel Reis. Wenn man z. B. einen Löffel eintaucht, kann man ab einer bestimmten Eintauchtiefe das Gefäß und den Inhalt anheben, indem man den Löffel festhält. Erklären Sie dieses Phänomen und untersuchen Sie die relevanten Parameter des Systems.

Statt einen Löffel haben wir einen Holzstab benutzt mit einer Flasche voller Sand. Wir haben das körnige Material variiert mit zwei unterschiedlichen Sandarten und zwei unterschiedlichen Holzstäben.

Theorie

Wir sehen ein einzelnes Sandkorn am Stab, mit den dort wirkenden Kräften.

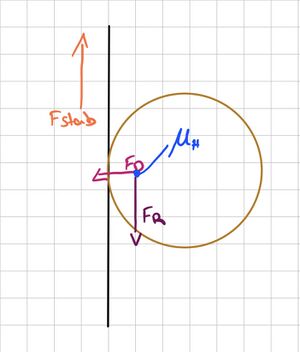
Unser Ziel war es ein Minimum $$F_{Stab}$$ mit

der Hilfe von $$ \sum_{F_R} $$ zu bestimmen. $$ F_{Stab} $$ muss größer sein als die gesamt Summe aller Sandkörner $$ \Sigma_{F_R} $$ , damit wir den Stab aus dem Sand ziehen können, müssen wir genügend Kraft aufwenden um die Reibungskraft $$ F_R $$ zu überwinden. $$F_R$$ können wir berechnen indem wir $$\mu_h$$, also den Haftreibungskoeffizenten mit $$F_D$$, der Kraft des Drucks multiplizieren. Das muss für jedes einzelne Sandkorn wiederholt werden. Weil jedes Sandkorn sein eigenes $$F_D$$, $$F_R$$ und $$\mu_h$$ hat. $$\mu_h$$ ist direkt abhängig von $$F_D$$. Um die unendlich vielen Sandkörner zu berechnen, könnte man Integrale verwenden.

Es ist zu sehen: eine Flasche mit Sand und Stab und dazu die wirkenden Kräfte.

Die Sandkörner sind zwischen Stab und Gefäßwand eingeklemmt. Ein Sandkorn drückt mit $$F_D$$ gegen den Stab. Das passiert von allen Seiten, womit der Stab eingeklemmt wird. Dort wirkt die Haftreibung. Zwischen den Sandkörnern haben wir Kraftbrücken, dass bedeutet, dass die Sandkörner gegen und aufeinander drücken. Auf jede Aktion folgt eine Reaktion. In unserem Fall ist die Aktion $$F_D$$ und die Reaktion ist die Gegenkraft, die auf die Gefäßwand vom Sand aus wirkt. $$F_R$$ wirkt nach unten in Richtung Gefäßboden, während unsere Aktion, also $$F_{Stab}$$ nach oben wirkt, da wir den Stab aus der Flasche raus ziehen wollen. $$F_D$$ bestimmen wir indem wir Kraft $$F$$ durch Fläche $$A$$ rechnen.

Formel:

$$F_D &=& \frac{F}{A}\$$

Omega

$

Aufbau

Mit diesem Aufbau wurden Eure Messungen durchgeführt. Dieser Abschnitt lebt von guten(!) Fotos bzw. Skizzen.

Anfängliche Aufbauten, die später verworfen wurden, können erwähnt werden aber müssen ausgiebig betrachtet werden.

Daten

Hier kommen keine Rohdaten sondern möglichst gut ausgewertete Daten rein - Graphen, Ausgleichskurven, etc. mit Fehlerbetrachtung!

Fazit

Eine kurze Zusammenfassung eurer Erkenntnisse.

Erfolge

Habt Ihr an Wettbewerben teilgenommen? Wie weit seid Ihr gekommen?

Quellen

Eure wichtigsten verwendeten Quellen mit Verweisen im Text!