HowTo Fourier

Diese Seite ist Work in progress!

Es wird immer wieder vorkommen, dass du auf periodische Phänomene triffst. Das können akustische oder elektromagnetische Schwingungen oder auch der veränderliche Wasserstand in einem Gefäß sein.

Abb. 1: Verlauf einer Harmonischen Schwingung

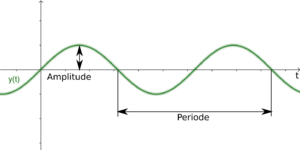
Aus dem Unterricht kennst du prinzipiell nur harmonische Schwingungen. Das sind solche, die sich durch eine Sinusfunktion beschreiben lassen, so wie inm Abb. 1 rechts

$$ y(t)=\hat y \sin\left(\frac{2\pi}{T} \cdot t\right).$$

Dabei ist die Auslenkung $$y(t)$$ komplett beschrieben durch den Zeitpunkt $$t$$, die Amplitude $$\hat y$$ und die Periode $$T$$. Einfacher noch mit der Kreisfrequenz $$\omega=\frac{2\pi}T$$:

$$ y(t)=\hat y \sin\left(\omega t\right).$$

Abb. 2: Verlauf einer nicht-harmonischen Schwingung

Abb. 3: einzelne Messwerte einer Schwingung

Das lässt aber komplett außer Acht, dass Schwingungen auch nicht-harmonisch sein können und der Graph einem allgemeineren Verlauf folgt (Abb. 2) oder dass anstatt des kompletten Graphen nur einzelne Messwerte, also Punkte auf dem Graphen vorliegen (Abb. 3).

Idee

Was eine harmonische und eine nicht-harmonische Schwingung gemeinsam haben, ist dass sie periodisch sind, also dass gilt $$y(t+T)=y(t)$$. Wenn eine Funktion $$y$$ aber $$T$$-periodisch ist, dann ist sie auch $$2T$$-, $$3T$$-, $$4T$$- usw. periodisch. Für harmonische - also sinusförmige - Schwingungen bedeutet das, dass nicht nur $$\sin\left(\omega t\right)$$ die Pariode $$T$$ hat sondern auch $$ \sin\left(2\omega t\right)$$, $$\sin\left(3\omega t\right)$$, $$\sin\left(4\omega t\right)$$ usw.

Die Idee von Joseph Fourier war jetzt, eine beliebige $$T$$-periodische Funktion als Summe von $$T$$-periodischen Sinusfunktionen darzustellen. Damit das Ganze mathematisch funktioniert, müssen auch noch passende Kosinusfunktionen mit dazu aber insgesamt konnte er zeigen, dass eine Summe

$$y(t)=\frac{a_0}2+a_1\cos\left(\omega t\right)+a_2\cos\left(2\omega t\right)+a_3\cos\left(3\omega t\right)+\ldots+b_1\sin\left(\omega t\right)+b_2\sin\left(2\omega t\right)+b_3\sin\left(3\omega t\right)+\ldots$$

prinzipiell jede $$T$$-periodische Funktion darstellen kann. (Wikipedia: Fourierreihe) (Das $$\frac{a_0}2$$ am Anfang wirkt vielleicht verwirrend, ist aber mathematisch nötig, damit alles klappt.)

Damit wird das aus der Akustik bekannte Prinzip von Grund- und Oberschwingungen auf beliebige Schwingungen übertragen. Jetzt besteht nur die Aufgabe darin, eine Funktion in eine Folge von $$a_k$$ und $$b_k$$ Werten umzuwandeln.

Fourier-Transformation

Der Weg, um von einer periodischen Funktion zu einer Folge von immer hochfrequenteren Sinus- und Kosinusfunktionen zu kommen, heißt Fourier-Transformation (engl. Fourier transform, FT). Die mathematischen Details sind in dem Wikipedia-Artikel: Fourierreihe zu finden. Hier werden wir sie nicht näher betrachten. Es soll reichen, dass es geht. Relevant für uns ist in der Regel auch der Fall, dass wir keine komplette Funktion zur Verfügung haben sodern nur eine Reihe von $$N+1$$ Messwerten in konstantem Abstand $$\Delta t$$. Auch für solche Listen von Werten kann eine Fourier-Transformation durchgeführt werden. Die gilt dann für exakt diese Messpunkte.

Beispiel:

$$t_i$$
$$y_i$$

Fallstricke

• Die FT liefert die Amplituden der Frequenzanteile von $$\omega_1=1\cdot\frac{2\pi}{\Delta t}$$ bis $$\omega_N=N\cdot\frac{2\pi}{\Delta t}$$. Dabei tritt aber ein Effekt auf, dass für Frequenzen oberhalb der sogenannten Nyquist-Frequenz $$f_{Ny}=\frac{f_{Abtast}}2$$ Wiederholungen auftreten. Konkret: $$a_k=a_{N-k}$$ und $$b_k=-b_{N-k}$$. Das heißt also, dass man aus einem Signal, das 100mal in der Sekunde abgetastet wird ($$f_{Abtast}=100$$Hz) keine Frequenzanteile herausholen kann, die größer als $$f_{Ny}=50$$Hz sind. Bildlich kann man sich das so vorstellen, dass eine Sinus-Schwingung von 50Hz, die mit 100Hz abgetastet wird, immer wechselnd +1 und -1 als Werte liefert und damit durchaus als Schwingung erkennbar ist. Tastet man sie mit 100Hz ab, wird genau ein Messwert pro Periode erfasst und man könnte stets bei +1 landen. Und das entspricht einer konstanten Funktion und keiner Schwingung mehr. Also Vorsicht! Wenn man eine Schwingung mit einer bestimmten Frequenz untersuchen will, muss man sie mit mindestens der doppelten Frequenz abtasten.
• Es gibt ein sehr schnelles Verfahren, eine FT durchzuführen. Dieses nennt sich Fast Fourier Transform (FFT) und basiert auf rekursiven Algorithmen - ähnlich wie Quicksort. Wenn jemand also von einer FFT spricht, macht er exakt das gleiche, wie bei einer FT - nur eben schnell. Aber man könnte als Opposition mal nachhaken und sich diesen (nicht vorhandenen) Unterschied zwischen Fast und Slow Fourier Transform erklären lassen.