Bottle Rocket Q2
Thema
IYPT Aufgabe auf Englisch
Pump air into a plastic water bottle partially filled with water. Under certain conditions, the bottle is launched and flies into the air. Investigate how the acceleration during lift-off depends on relevant parameters.
IYPT Aufgabe übersetzt
Pumpen Sie Luft in eine teilweise mit Wasser gefüllte Plastikflasche. Unter bestimmten Bedingungen wird die Flasche starten und fliegt in die Luft. Untersuchen Sie, wie die Beschleunigung beim Abheben von relevanten Parametern abhängt.
Worum geht es hier?
In dieser Arbeit wird die Beschleunigung einer Wasserrakete während des Starts vorgestellt. Dabei fokussieren wir uns auf die unterschiedlichen Wasser Mengen in der Flasche/Rakete und die daraus folgenden Veränderungen der Beschleunigung.
Theorie
Annahmen
(0)
• Reibungsfreie Strömung
• Stationäre Strömung
• Inkompressibles Fluid
Unsere Parameter
• Volumen der Flasche (leer/gefüllt)
• Gewicht der Flasche (leer/gefüllt)
• Durchmesser der Flasche/Öffnung
• Innendruck $$p$$ (bzw. die Differenz zum Außendruck)
• Impuls $$p$$
• Schubkraft $$T$$
• Luftreibungskraft $$F_F$$
Allgemeine Erläuterung
Zu Beginn des Experiments wird die genutzte Flasche mit Wasser befüllt, was zu einem Überdruck innerhalb der Rakete führt. Der Innendruck ist also höher als der Außendruck. Aufgrund dieses Druckunterschiedes entsteht eine Gradientkraft, welche den Druck ausgleicht. Dabei ist diese gegen die Flasche aber auch das Wasser gerichtet, da sie von einem Bereich der höheren Luftkonzentration zu einem Bereich einer niedrigeren Luftkonzentration gerichtet ist. Da die Flasche zu diesem Zeitpunkt noch geschlossen ist, und das Material auf die Gradientkraft mit einer mechanischen Spannung im Material reagiert, kommt es nicht zum Druckausgleich. Dieser erfolgt erst, sobald die Flasche geöffnet ist. Daraufhin strömen das Wasser sowie die Luft aus der Flasche, da die Öffnung in Richtung Erdoberfläche gerichtet ist. Damit die Flasche nun vertikal nach oben fliegt, muss ihre Beschleunigung ($$a$$), welche durch die Schubkraft ($$T$$) verursacht wird, die Gravitationskraft ($$F_G$$) überwinden. So kann die Rakete mit einer resultierenden Kraft ($$F_r$$) nach oben fliegen. Diese werden wie folgt berechnet:
1. Gravitationskraft:
$$F_G=m∙g$$ (1)
$$F_G$$ Gravitationskraft
$$m$$ Masse der Flasche
$$g$$ Erdbeschleunigung (=9,81 $$m/s^2$$ )
2. Schubkraft:
$$T=v᛫dm/dt$$ (2)
$$T$$ Schubkraft
$$v$$ Geschwindigkeit der Rakete nach oben
$$dm$$ Änderung der Masse
$$dt$$ Änderung der Zeit
3. Resultierende Kraft:
$$F_r=T-F_G$$ (3)
$$F_r$$ Resultierende Kraft
$$T$$ Schubkraft ↑
$$F_G$$ Gravitationskraft ↓
4. Luftreibungskraft: $$F_F=1/2 ρv^2 C_D A$$ (4)
$$F_F$$ Luftreibungskraft
$$ρ$$ Dichte des Fluids
$$C_D$$ Strömungswiderstandskoeffizient
$$A$$ Querschnittsfläche
$$v$$ Geschwindigkeit des Körpers relativ zum Fluid
(Ein Teil des folgenden Absatzes stammt aus unserer Facharbeit für Jugend Forscht 2025)Kleiner Text
Um nun aber zu erklären, wie die Schubkraft ($$T$$) zustande kommt bzw. weshalb sich die Flasche überhaupt bewegt, wird nun die Impulserhaltung betrachtet. Diese besagt, dass der Impuls vor dem Öffnen der Flasche gleich dem Impuls nach dem Öffnen der Flasche ist.
Dabei gilt für den Impuls:
$$p=m∙v$$ (5)
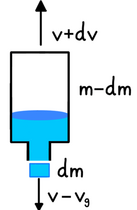
Da die Geschwindigkeit ($$v$$) der Wasserrakete vor dem Öffnen 0 beträgt ($$p_v$$), ist der Impuls 0, und der Impuls nach Öffnung ($$p_n$$) des Schließmechanismus muss ebenfalls 0 betragen. Der Impuls ($$p$$) nach dem Öffnen ergibt sich aus dem Impuls ($$pr$$) der Rakete nach oben und dem Impuls ($$pT$$) des ausströmenden Wassers nach unten. $$P_T$$ ist das Produkt der Masse des ausgeströmten Wassers ($$dm$$) und der Geschwindigkeit der austretenden Reaktionsmasse ($$v_g$$) subtrahiert von der Anfangsgeschwindigkeit ($$v=0$$).
$$0=p_v=p_n=p_R+p_T$$ (6)
$$0=(m-dm)∙(v+dv)+dm∙(v-v_g)$$ (7)
Da die Geschwindigkeit des Treibstoffs negativ ist, gilt:
$$0=(m-dm)∙dv-dm×v_g$$ (8)
Somit gilt:
$$dv=(dm∙v_g)/(m-dm)$$ (9)
Außerdem besagt die Kontinuitätsgleichung, dass, je kleiner die Fläche der Öffnung $$A$$, desto höher die Strömungsgeschwindigkeit $$v$$:
$$A_1∙v_1=A_2∙v_2$$ (10)
Zusammenfassend kann man sagen, dass sich die Rakete mit der Geschwindigkeit $$dv$$ nach oben bewegt, da durch die Gradientkraft in der Flasche die Wassermasse aus der Flasche stark gedrückt wird und die Impulserhaltung auch in die entgegengesetzte Richtung wirken muss. Diese Geschwindigkeit ist auch größer, wenn die Öffnung der Flasche kleiner ist.
Untersuchung der Beschleunigung
Nun wird die, nach der Aufgabenstellung, gesuchte Beschleunigung genauer untersucht. Um die genaue Beschleunigung der Rakete zu ermitteln, ist es erst einmal nötig festzustellen, welche Beschleunigungen gegeneinander wirken. In diesem Fall, der Rakete, ergibt sich die resultierende Beschleunigung der Rakete wie folgt:
$$a=a_I-g-a_F$$ (11)
$$a$$ resultierende Beschleunigung
$$a_I$$ Schubbeschleunigung
$$g$$ Erdbeschleunigung
$$a_F$$ Beschleunigung des Luftwiderstandes
Um diese Beschleunigung ($$a$$) zu bestimmen, ist es nötig, die einzelnen Variablen genauer zu betrachten. Dabei lässt sich die Beschleunigung des Luftwiderstandes mit Hilfe der Luftreibungskraft aus (4) bestimmen, dabei gilt folgendes:
$$F_F=D∙v^2$$ (12)
wobei D für eine Konstante, die wie folgt definiert wird, steht:
$$D≔1/2 ρ_L∙c_D∙A$$ (13)
Mit des 2. Newton´schen Axioms:
$$F=m∙a$$ (14)
welches besagt, dass die Masse ($$m$$) eines Körpers multipliziert mit seiner Beschleunigung ($$a$$) die Kraft ($$F$$) ergibt, welche auf diesen Körper wirkt, lässt sich nun die gesuchte Beschleunigung, die Beschleunigung des Luftwiederstandes ($$a_F$$) ermitteln:
$$a_F=F_F/m=D/m v^2$$ (15)
Um die Schubbeschleunigung ($$a_I$$) zu berechnen, kann man die erste Ableitung der Geschwindigkeit (v ̇) „über der Zeit“ berechnen. Diese lässt sich aber auch anders schreiben, da die Rakete über das Zeitintervall (dt) den Massenanteil (dm) in Form von Treibstoff mit der Austrittsgeschwindigkeit ($$v_g$$) verliert. Daraus geht aufgrund der Impulserhaltung diese Geschwindigkeitszunahme (dv) der Rakete hervor:
$$dv=-v_g∙m^(-1)×dm$$ (16)
Daraus folgt schließlich die eigentliche Schubbeschleunigung ($$a_I$$):
$$a_I=-dm/dt∙v_e/m=dv/dt=v$$ ̇ (17)
Des Weiteren spielt auch noch die konstante Erdbeschleunigung ($$g$$) von $$9,81 m/s^2$$ eine Rolle, um die finale Beschleunigung zu berechnen.
Die finale Gleichung, um die Beschleunigung nun zu bestimmen, sieht also wie folgt aus:
$$a=a_I-g-a_F=(v_g dm)/mdt-g-D/m v^2$$ (18)
Es fällt auf, dass die Geschwindigkeit der austretenden Reaktionsmasse $$(v_g)$$, welche Teil der finalen Gleichung ist, noch nicht bestimmt werden kann. Dies wird aber im folgenden Teil mit Rückgriff auf die Bernoulli-Formel getan, diese kann unter Rücksicht der Annahmen (0) genutzt werden, wobei:
$$ρ∙g∙h+1/2∙v_g^2∙ρ+p=const.$$ (19)
ein klassischer Fall der Bernoulli-Gleichung aus der Stömungsmechanik ist. Dabei versteht man unter ($$p$$) den statischen Druck, ($$ρ$$) die Dichte des Fluids, ($$g$$) die Erdbeschleunigung, ($$Δp$$) den Druckunterschied innerhalb/außerhalb der Flasche und ($$h_w$$) die Höhe des Fluids. Nach Umstellung von (19) erfolgt:
$$v_g=√((2∙△p)/ρ+g∙h_w)$$ (20)
Nun ist die Geschwindigkeit der Reaktionsmasse berechenbar, was dazu führt, dass die finale Gleichung der Theorie (18) ebenfalls berechenbar ist.
Aufbau
Der Versuchsaufbau & die Skizze
Unser Versuchsaufbau besteht aus einem Seil, das wir vom Balkon der Schule hängen lassen. Am unteren Ende des Seils ist ein 5kg Gewicht befestigt, damit das Seil straff hängt. Um das Seil ist ein Metallrohr befestigt, an das eine Wasserflasche verkehrt herum befestigt ist. Auf den Flaschenboden wird ein Beschleunigungssensor (Vernier) sicher befestigt. In die Öffnung der Flasche wird ein Plastikrohr, das mit einem Schaumstoff Kegel ummantelt und mit einem Kondom überzogen ist, gesteckt, um diese zu verschließen. Dies ist mithilfe eines Gartenschlauchverbindungsstücks und einem Stück Schlauch mit dem Kompressor verbunden.
Die Versuchsdurchführung
In die Flasche wird Wasser gefüllt und die Öffnung wird anschließend verschlossen. Mit Hilfe des Kompressors wird Luft in die Flasche gepumpt. Die Stopfen löst sich, wenn zu viel Druck in der Flasche ist, wodurch die Flasche anfängt zu starten und somit auch zu beschleunigen. Der Vernier Beschleunigungssensor misst die Beschleunigung und ist mit einem Handy verbunden. In der App von Vernier werden die Messdarten der Beschleunigung angezeigt.
Daten
Im Folgenden werden die Ergebnisse der Experimente vorgestellt.
Experimente mit Vernier
Mithilfe des Beschleunigungssensors sind Graphen wie diese entstanden:
Auf der x-Achse ist die Zeit in Sekunden angegeben und auf der y-Achse die Beschleunigung in Meter pro Quadratsekunde. Den Graphen kann man in mehrere Phasen teilen. Von 0s bis ca. 0,9s bewegt sich die Flasche noch nicht. Da der Sensor die Erdbeschleunigung von 9,81m/s^2 rausrechnet, wird die Normalkraft mit der entgegengesetzten Beschleunigung angezeigt. Dies muss man beim Betrachten von diesem Graphen im Hinterkopf behalten. Die zweite Phase beginnt bei dem Anstieg des Graphen und endet bei dem Sinken des Graphens auf 9,81m/s^2. Diese Phase zeichnet die Beschleunigungsphase aus. In dieser Phase beschleunigt die Rakete wegen dem ausströmenden Wasser und anschließender Luft. Der erste Teil dieser Beschleunigung erfolgt mit dem Wasser. Am Ende dieser Phase beschleunigt die Flasche weniger, bis sie nicht mehr schneller wird.
Den Bogen kann man mit dem Zusammenspiel zweier Faktoren erklären. Durch die weniger werdende Masse der Flasche wird über Zeit die Beschleunigung der Flasche höher. Auf der anderen Seite wird der Druck in der Flasche auch weniger, wodurch die Beschleunigung wieder kleiner wird.
Ab dem Punkt der Nicht-Beschleunigung wird die Flasche langsamer und fällt anschließend mit einer Beschleunigung von 9,81m/s^2 runter, bis sie auf dem Ende des Seils trifft.
Der Experimente Theorie Vergleich
Die Messergebnisse können teilweise mit der Theorie verglichen werden. Die Theorie bezieht sich nur auf die Beschleunigungsphase durch das Wasser, bis das Wasser nach der Simulation aus der Flasche ist. Im folgenden wird der Vergleich gezeigt.
Bei diesem Vergleich sieht man, dass die Theorie relativ gut passt. Da die Simulation und Messwerte in 0,01s Schritte erfolgt, und die Zeit, bis das Wasser aus der Flasche raus ist, ziemlich kurz ist, sieht man die Ecken im Graphen der Theorie. Trotzdem ist das Wasser ungefähr zur gleichen Zeit aus der Flasche wie wir es erwartet haben. Die Höhe der erreichten Beschleunigung des ersten Peaks könnte unsere Vermutung bestätigen, dass die Beschleunigung des Wassers bis zum ersten Peak erfolgt und danach mit der Luft.
Messungen mit verschiedenen Volumen
Darauffolgend wurde der Durchschnitt aller Maximalbeschleunigungen für verschiedene Volumen aufgenommen und in einem Graphen zusammengefasst.
In diesem Graphen erkennt man näherungsweise einen Bogen nach oben. Dies liegt an ein weiteres Zusammenspiel von 2 Faktoren. Ein höheres Volumen bedeutet eine höhere Masse. Dadurch besteht auch eine höhere Gewichtskraft, die überwinden werden muss, wodurch die Beschleunigung kleiner ist. Dennoch gibt es bei einem kleinen Volumen auch weniger Masse, was mit einer niedrigeren Schubkraft resultiert, wodurch eine kleinere Beschleunigung vorhanden ist. Das „perfekte“ Volumen, also das Volumen, wodurch die höchste Beschleunigung erreicht wird, ist also zwischen 150 und 250ml.
Fazit
Das Projekt befasst sich mit der Beschleunigung einer Wasserrakete. Anhand der Theorie konnten wir die Beschleunigung mit dem Wasser rekonstruieren. Außerdem konnten wir mit unseren Experimenten die gesamte Beschleunigungsphase näher betrachten.
Dieses Projekt war im Groben und Ganzen erfolgreich und gelungen. Im gesamten Prozess von diesem Projekt haben wir unseren Aufbau mehrmals optimiert, unsere Theorie weiterentwickelt und gelernt, Daten auszuwerten und zu interpretieren.
Erfolge
2x BeGYPT Beiteiligung mit einem 2. Platz als Team
1x GYPT-Bundeswettbewerb Nominierung
Jugend Forscht Regional Wettbewerb 3. Platz
Danksagung
Wir bedanken uns bei:
– Herrn Ebert für seine Unterstützung bei der Ideen Findung und seiner Kritik, die uns geholfen hat, motiviert zu bleiben
– Lilli Roters als Betreuerin, die uns mit Tips und Ratschlägen geholfen hat, nicht zu verzweifeln
– Unseren Mitschülern, die uns durch ihr Hinterfragen bei den Präsentationen immer neue Denkanstöße gegeben haben
Quellen
On the approximation of D.I.Y. water rocket dynamics including air drag (by L. Fischer, T. Günther, L. Herzig, T. Jarzina,
F. Klinker, S. Knipper, F.-G. Schürmann, M. Wollek ): https://arxiv.org/pdf/2001.08828