Luftmuskel

Thema

An einem Stativ wird ein Ballon befestigt, welcher von einem Netz (z.B ein Knoblauch Netz) umgeben ist. Es wird gezielt mithilfe eines Luftkompressors der Ballon zum Expandieren gebracht, wodurch sich das Netz verkürzt, weshalb man diesen Aufbau als eine einfache Nachahmung eines Muskels sehen kann. Es soll untersucht werden wie sich die Dimensionen des Netzes ändern und wie hoch die Zugkraft dieser Kontraktion ausfallen kann.

Theorie

Parameter

Wichtige Parameter, welche in unserem Experiment vorgekommen sind:

$$F$$ Zugkraft des Luftmuskels

$$p$$ Druck innerhalb des Ballons

$$V$$ Volumen des Ballons(Der Ballons wurde als verlängertes Rotationsellipsoid gesehen)

$$T$$ Temperatur während des Experiments

$$R_{s}$$ die spezifische Gaskonstante für Luft

$$∆l$$ Verkürzung des Netzes

$$a$$ Der Radius des Äquatorkreises beim Rotationsellipsoid

$$c$$ Der Abstand der Pole vom Mittelpunkt beim Rotationsellipsoid

Abb.1 Die zeitliche veränderung des Innendrucks bei einem Luftballon

$$m$$ die Masse des Gases

Verkürzung des Ballons und Kraftausübung

Zuerst wird nachvollzogen warum der Ballon eine Kraft auf das Netz ausübt. Dies lässt dadurch erklären, dass durch die Luftzufuhr der Druck innerhalb des Ballons erhöht wird, wodurch sich dessen Material ausdehnt. Ein interessanter Fakt ist hierbei, dass der Druck in einem Luftballon nicht linear ansteigt mit steigendem Ballonradius sondern sich eher so wie in Abb. 1 dargestellt verhält. Als zweites wird die Struktur des Netztes analysiert, wobei auffält, dass dieses rautenförmige Löcher aufweist, welche entlang des Ballonumfangs gestreckt werden, wenn man den Ballon mit luft befüllt (siehe Abbildung 2). Diese Streckung wird durch Kräfte verursacht, welche wie folgt an den mittleren Rauten des Netzes wirken:

Abb.2 Netzstruktur ohne und mit aufgeblasenem Ballon + wirkende Kräfte auf ein Teil des Netzes während man den Ballon aufbläst

Im eigentlichen Experiment:

Grüner Kraftpreil = Senkrecht vom Netz weg

Blauer Kraftpfeil = Zum Zentrum der Löcher

Grauer Kraftpreil = Entlang des Ballonumfangs

Da dieser Prozess eine Materialzufuhr von beiden Enden des Netzes verlangt, verkürzt sich dieses während der Durchmesser in der Mitte dessen wächst. Dadurch wirkt eine Kraft vom Ballon über das Nezt auf die Netzenden, durch welche sie zur Netzmitte gezogen werden.

Abb.3 verlängertes Rotationsellipsoid [Q1]

Der innendruck des Ballons lässt sich mithilfe der algemeinen Zustandsgleichung $$pV = mR_{s}T$$ berechnen, wobei sich die Gleichung $$p = \frac{mR_{s}T}{V}$$ ergibt (Hierbei steht $$p$$ für den Druck, $$V$$ ist das Volumen, $$m$$ die Masse, $$R_{s}$$ die spezifische Gaskonstante für Luft und $$T$$ die Temperatur). Da Druck nichts anderes als Kraft pro Fläche ist also $$\frac{F}{A}$$ kann man die Gleichung folgendermaßen aufschreiben $$\frac{F}{A} = \frac{mR_{s}T}{V}$$. Nun lässt sich erkennen, dass sowohl die Kraft als auch der Druck von ähnlichen Parametern abhängig sind und gleichermaßen von denen beeinflusst werden, wodurch bei einer graphischen Darstellung des Drucks in Abhängigkeit von der Kraft, der Graph sich linear verhalten sollte.

Um die Veränderung der Netzform beschreiben zu können sehen wir das Netz als auch den Ballon als verlängerte Rotationsellipsoide (siehe Abb.3). Somit gelten folgende Formeln für diese:

Volumen: $$V = \frac{4π}{3}a^2 c$$

Oberfläche: $$A = 2πa(a + \frac{c^2}{\sqrt{c^{2} - a^{2}}}\arcsin(\frac{\sqrt{c^{2} - a^{2}}}{c}))$$

Aufbau

Der Aufbau in der unten dargetellten Abb4 war eine Zusammenstellung unsere ersten Ideen um die Umsetzbarkeit des Systems zu prüfen und auch die maximale mögliche Kraft herauszufinden, wobei wir aber später merkten, dass die maximale Kraft des Netzes, die des Kraftmessers übertraf. Also erweiterten wir den Aufbau über 2 Tische hinweg mit einem Hebel ( siehe Abb5 ). Zudem merkten wir auch, dass verschiedene Netze verschiedene Zugkräfte erwiesen, also probierten wir mehrere aus und entschlossen uns auf das Netz der Marke "Reine", die eine maximale Zugkraft von über 50 Newton erwies.

Abb.5 - Erweiterter Aufbau zur Kraftmessung mit Hebel

Abb.4 - Aufbau zur Kraftmessung ( erste Theoriewerte )

Der in Abb5 abgebildete Aufbau ist eine Erweiterung dessen davor, indem der Kraftmesser mit einer Umlenkrolle ersetzt wurde und der Nylonseil so über dem Tisch gehangen wird, dass eine befestigte Tasche, die ein Gewicht enthält, genau den Boden berührt. Bei einer Erhöhung des Innendrucks steigt der Durchmesser und, wie schon in der Theorie erwähnt, führt eine benötigte Materialzufuhr dann zu einer Verkürzung des Netzes. Diese Verkürzung △ls des Ballons führt zu einer Erhebung des Massestücks, die wir dann erstmal mit Papier und Büchern gemessen haben und danach mit einem feinen Messgerät genau in eine Tabelle eingetragen haben. Die Masse erhöhten wir in 500 gramm Abständen von 0.5kg bis 5kg.

Abb.6 - Aufbau zur Messung △l

Daten

Innendruckmessung

Zuerst die Änderung des Balloninnendrucks in unserem Aufbau zur Messung der maximalen Zugkraft:

Abb.7 - Graphische Darstellung des Innendruckverlaufs, während einer Kraftmessung, wobei dieser als Überdruck angegeben ist.

Man kann erkennen, dass der Überdruck dauerhaft ansteigt mit einer kleinen "Ausnahme" am Anfang, wobei er am Ende einen maximalen Wert von ungefähr 18kPa erreicht. Diese "Ausnahme" lässt sich dadurch erklären, dass der Ballon zunächst keinen Kontakt mit dem Netz hat und somit ersteinmal die vom Innendruck zu erreichende Schwelle, damit der Ballon anfängt sich stärker auszudehen, nur vom Ballonmaterial bestimmt wird. Während diese Schwelle errreicht wird dehnt sich der Ballon nur sehr langsam aus aber diese leichte Ausdehnung reicht aus, sodass der Ballon mit dem Netz in Kontakt kommt und nun eine  Gegekraft vom Kraftmesser auf den Ballon ausgeübt wird, wenn dieser wächst. Dadurch sinkt der Druck nicht wieder, wie es bei einem freien Luftballon der Fall wäre, sondern muss weiterhin ansteigen, damit sich der Ballon weiter ausdehnt. Die Fehlerechnung ergab hier einen Fehlerbereich von $$\pm2kPa$$, welchen die Fehlerindikatoren darstellen.

Zugkraftmessung

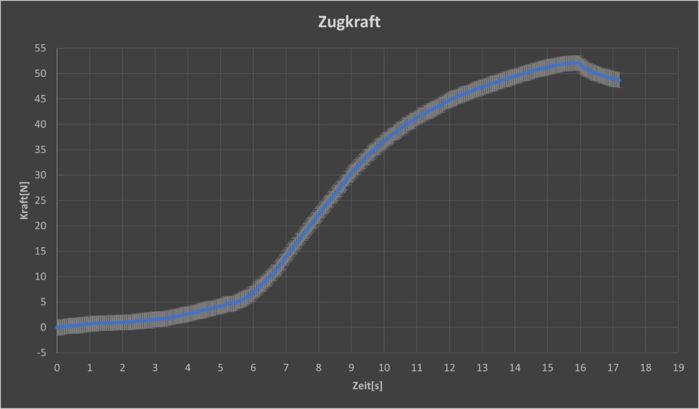
Die Zugkraft, welche während der Oben gezeigten Druckmessung vom Kraftsensor gemessen wird, verläuft folgendermaßen:

Abb.8 - Graphische Darstellung des Kraftverlaufs während der Ballon aufgepumpt wurde

Man kann erkennen, dass der Verlauf der Zugkraft stark dem des Innendrucks ähnelt, dies wurde in unserer Theorie erklärt, allerdings lässt sich auch erkennen, dass die Zugkraft erst später anfängt anzusteigen, weil der Ballon ersteinmal so gut wie keinen Kontakt mit de Netz hat, wodurch er noch nicht vollstädig eine Kraft auf das Netz ausüben kann. Nachdem der Ballon sich stark genug ausgedehnt hat fängt die Zugkraft an zu steigen. Die maximale Zugkraft beträgt hier ca. $$52N$$. Durch die Fehlerrechnung ergab sich ein Fehlerbereich von ca. $$\pm1,5N$$.

Zusammenhang Zugkraft und Innendruck

Um nun den Zusammenhang zwischen dem Innendruck und der Zugkraft besser erkennen zu können ist hier ein Diagramm, welches die wirkende Zugkraft in abhängigkeit des Innedrucks darstellt:

Abb.9 - Graphische darstellung des Zusmmenhngs zwischen Zugkraft und Balloninnendruck mit den entspechenden Fehlerbalken

Hier kann man nochmal erkennen, dass ab ca. 9kPa eine linearität vorliegen könnte. Der bereich davor lässt sich wie oben beschrieben mit dem fehlenden Kontakt erklären, aber nach einem Innendruck von 9kPa ist es keine sieht es nicht wie echte Linearität aus, wodurch unsere Theorie falsch wäre. Allerdings lassen sich die Unrgelemäßigkeiten im Graphen dadurch erklären, dass, aufgrund der auftretenden Reibung zwischen dem Ballon und Netz(Ballon denht sich aus, wodurch sich der Ballon und das Netz an den Kontaktstellen in unterschiedliche Richtungen bewegen), das Netz immer wieder für einen kurzen Moment ruckartig vom Ballon rutscht und dabei der Ballon kurzzeitig keinen Kontakt an dieser stelle mit ihm hat.

Eine weitere wichtige Sache die man zu den Abbildungen 7 und 8 hinzufügen muss ist, dass diesen in Abhängigkeit der Zeit dargestellt sind also jeglichen genauen Werte zur Steigung, Anfang und Ende der Werte davon abhängig waren, wie gleichmäßig und schnell der Ballon mit Luft befüllt wurde und wann die Messung gestartet wurde.

Verkürzung

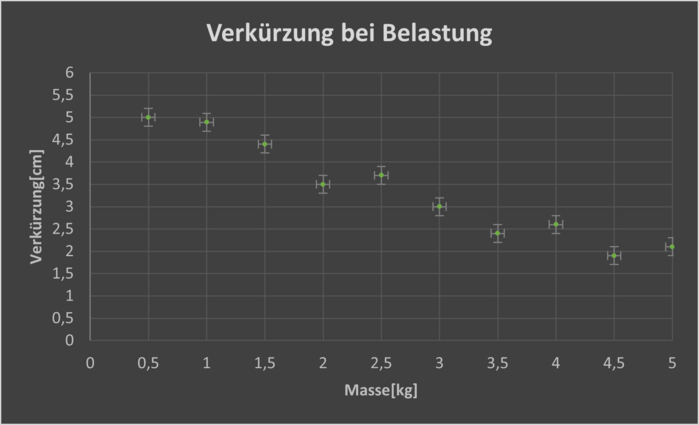
Des Weiteren haben wir noch gemessen, wie sich die Verkürzung des Netzes bei variierender Belastung aber gleichem Innendruck verhält:

Abb.10 - Graphische Darstellung der Netzverkürzung bei steigender drangehängter Masse mit dazugehörigen Fehlerindikatoren

Man kann gut erkennen, dass sich das Netz immer weniger verkürzt, wenn man mehr Masse dranhängt. Die Ausreißer lassen sich wahrscheinlich, dadurch erklären, dass es uns noch an weiteren Messreihen hierzu fehlt, um eine aussagekräftigere Darstellung des Zusammenhangs zwischen Belastung und Verkürzung erstellen zu können. Allerdings sollte sich auch bei weiteren Messreihen nicht ändern, dass grundsätzlich die Verkürzung mit zunehmender Belastung geringer ausfällt, da mit höherer Masse eine stärkere Gegenkraft auf den Ballon ausgeübt wird und der Innendruck immer auf einen festen Wert erhöht wird, sodass der Ballon bei einer höheren Masse ein kleineres Volumen haben wird (sobald der festgelegte Innendruck erreicht wird) als bei einer niedrigeren Masse und damit die Verkürzung des Netzes geringer ausfällt. Die vorhandenen Fehlerindikatoren stellen einen Fehlerbereich von $$\pm0,057Kg$$ bei der Masse und $$\pm0,2cm$$ bei der Verkürzung dar.

Fazit

Die Untersuchung hat gezeigt, dass ein Luftballon, der in einem Netz expandiert, eine wirkungsvolle Nachahmung eines Muskels darstellt. Durch die gezielte Luftzufuhr mittels eines Kompressors dehnt sich der Ballon aus und übt eine Zugkraft über das Netz aus, was zu einer Verkürzung des Netzes führt. Dieser Prozess wurde sowohl theoretisch als auch experimentell untersucht.

Die wichtigsten Erkenntnisse aus dem Experiment sind:

- Druck und Zugkraft: Es konnte bestätigt werden, dass der Innendruck des Ballons und die daraus resultierende Zugkraft auf das Netz direkt miteinander korrelieren. Der Druckanstieg im Ballon führt zu einer Zunahme der Zugkraft, die auf das Netz ausgeübt wird. Diese Beziehung zeigte sich ab einem Innendruck von ca. 9kPa als nahezu linear.

- Maximale Zugkraft: Die experimentellen Messungen ergaben eine maximale Zugkraft von etwa 52N, wobei die verwendeten Netze unterschiedliche Zugkräfte aufwiesen. Das Netz der Marke "Reine" zeigte die höchste Zugkraft.

- Materialverkürzung: Die Verkürzung des Netzes variiert mit der angehängten Masse, wobei eine größere Masse zu einer geringeren Verkürzung führt, da bei einer höheren Masse eine höhere Gegenkraft auf den Ballon ausgeübt wird und damit der Ballon ein kleineres Volumen haben wird ( sobald der festgelgte Innendruck erreicht wurde) als bei einer niedrigeren Masse, sodass die Verkürzung des Netzes geringer ausfällt.

Insgesamt konnte durch das Experiment das Verhalten eines Luftballons in einem Netz als Modell für die Kontraktion eines Muskels erfolgreich simuliert und analysiert werden. Die Erkenntnisse bieten eine Grundlage für weitere Untersuchungen und Optimierungen dieses Modells, um ein besseres Verständnis der zugrunde liegenden physikalischen Prinzipien zu gewinnen.

Erfolge

• Jugend Forscht Regionalwettbewerb Berlin Nord zweiter Preis im Bereich Technik.

• Sonderpreis Besuch im DLR Schullab
• Sonderpreis “Ausstellung bei der langen Nacht der Wissenschaft”

Quellen

https://de.wikipedia.org/wiki/Rotationsellipsoid#/media/Datei:Ellipsoid-rot-ax.svg [Q1]